
 如图,任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,给四边形ABCD添加一个条件,使四边形EGFH是菱形,你添加的一个条件是AB=CD.请加以说明.
如图,任意四边形ABCD中,点E、F、G、H分别是AD、BC、BD、AC的中点,给四边形ABCD添加一个条件,使四边形EGFH是菱形,你添加的一个条件是AB=CD.请加以说明. 分析 由邻边相等的平行四边形是菱形可以得到:当EG=EH时,平行四边形EGFH是菱形.
解答 解:需添加条件AB=CD.理由如下:
∵E,G是AD,DB中点,
∴EG∥AB,EG=$\frac{1}{2}$AB,
∵H,F是AC,BC中点,
∴HF∥AB,HF=$\frac{1}{2}$AB,
∴EG∥HF,EG=HF,
∴四边形EGFH是平行四边形,
∵E,H是AD,AC中点,
∴EH=$\frac{1}{2}$CD,
∵AB=CD,
∴EG=EH,
∴四边形EGFH是菱形.
故答案为:AB=CD.
点评 此题主要考查了三角形中位线定理与菱性的判定方法,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
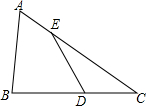 如图,D、E分别为△ABC边BC、AC上一点,证明:$\frac{{S}_{△ABC}}{{S}_{△ECD}}$=$\frac{AC•BC}{EC•CD}$.
如图,D、E分别为△ABC边BC、AC上一点,证明:$\frac{{S}_{△ABC}}{{S}_{△ECD}}$=$\frac{AC•BC}{EC•CD}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com