
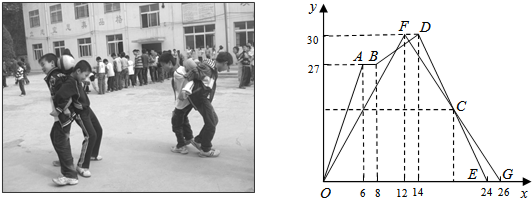
分析 (1)根据函数图象的纵坐标为30,可得这是一次60米的背夹球比赛,利用横坐标可得,获胜的是甲组同学;
(2)因为从A到B的路程不变,所以甲组两位同学在比赛中掉了球,因为从A到B的时间为2秒,所以线段AB的实际意义是甲组两位同学在比赛中掉了球,耽误了2秒;
(3)根据点F,G的坐标,求出直线FG的函数解析式,根据点D,E的坐标,求出直线DE的函数解析式,然后组成方程组,求方程组的解,即为C的坐标,即可解答.
解答 解:(1)根据函数图象可得这是一次60米的背夹球比赛,获胜的是甲组同学;
(2)因为从A到B的路程不变,所以甲组两位同学在比赛中掉了球,因为从A到B的时间为2秒,
所以线段AB的实际意义是甲组两位同学在比赛中掉了球,耽误了2秒.
(3)设直线FG的函数解析式为:y=k1x+b1,
把F(12,30),G(26,0)代入y=k1x+b1 得:$\left\{\begin{array}{l}{12{k}_{1}+{b}_{1}=30}\\{26{k}_{1}+{b}_{1}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=-\frac{15}{7}}\\{{b}_{1}=\frac{390}{7}}\end{array}\right.$,
∴直线FG的函数解析式为:y=-$\frac{15}{7}$x+$\frac{390}{7}$;
设直线DE的函数解析式为:y=k2x+b2,
把D(14,30),E(24,0)代入y=k1x+b1 得:$\left\{\begin{array}{l}{14{k}_{2}+{b}_{2}=30}\\{24{k}_{2}+{b}_{2}=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=-3}\\{{b}_{2}=72}\end{array}\right.$,
∴直线DE的函数解析式为:y=-3x+72,
∴得到方程组$\left\{\begin{array}{l}{y=-\frac{15}{7}x+\frac{390}{7}}\\{y=-3x+72}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=19}\\{y=15}\end{array}\right.$,
∴C的坐标(19,15)
∴说明点C的实际意义是当比赛进行到19秒时,甲、乙两组同学离终点均为15米.
点评 本题考查了一次函数的应用,解决本题根据是读懂函数图象,然后用待定系数法求一次函数的解析式,组成方程组求交点坐标.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | -5<t<-2 | B. | t>-2 | C. | -2<t<5 | D. | t>-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
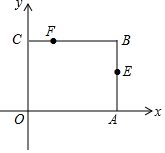 如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.
如图,矩形OABC放在以O为原点的平面直角坐标系中,A(3,0),C(0,2),点E是AB的中点,点F在BC边上,且CF=1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 区县 | 大兴 | 通州 | 平谷 | 顺义 | 怀柔 | 门头沟 | 延庆 | 昌平 | 密云 | 房山 |
| 最高气温 | 32 | 32 | 30 | 32 | 30 | 32 | 29 | 32 | 30 | 32 |
| A. | 32 | B. | 31 | C. | 30 | D. | 29 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
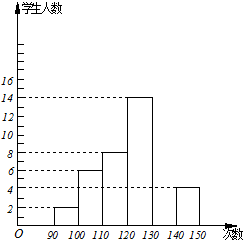 某学校为了了解八年级500名男生体能的情况,从中随机抽取了部分男生进行1分钟跳绳次数测试,将数据整理后,绘制成如下不完整的频数分布表和频数分布直方图:
某学校为了了解八年级500名男生体能的情况,从中随机抽取了部分男生进行1分钟跳绳次数测试,将数据整理后,绘制成如下不完整的频数分布表和频数分布直方图:| 分组 | 频数 | 频率 |
| 90≤x<100 | 2 | 0.04 |
| 100≤x<110 | 6 | 0.12 |
| 110≤x<120 | 8 | b |
| 120≤x<130 | 14 | 0.28 |
| 130≤x<140 | a | 0.32 |
| 140≤x<150 | 4 | 0.08 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 一定是正面朝上 | B. | 一定是正面朝下 | ||
| C. | 正面朝上的概率为0.8 | D. | 正面朝上的概率是0.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 每周课外阅读时间(小时) | 0~1 | 1~2(不含1) | 2~3(不含2) | 超过3 |
| 人 数 | 7 | 10 | 14 | 19 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com