
【题目】在![]() 和
和![]() 中,
中,![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.
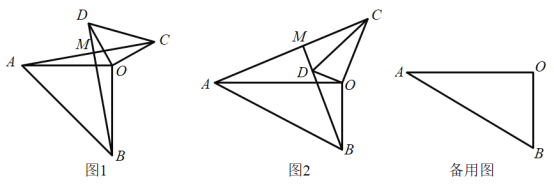
(1)如图1,若![]() ,填空:①
,填空:①![]() 的值为____________;
的值为____________;
②![]() 的度数为___________.
的度数为___________.
(2)如图2,若![]() ,求
,求![]() 的值(用含
的值(用含![]() 的式子表示)及
的式子表示)及![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,
,![]() ,将三角形
,将三角形![]() 绕着点
绕着点![]() 在平面内旋转,直接写出当点
在平面内旋转,直接写出当点![]() 、
、![]() 、
、![]() 在同一直线上时,线段
在同一直线上时,线段![]() 的长.
的长.
【答案】(1)①1;②![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)①先根据等腰三角形的判定与性质可得![]() ,再根据三角形全等的判定定理与性质即可得;
,再根据三角形全等的判定定理与性质即可得;
②先根据①三角形全等的性质可得![]() ,再根据直角三角形的性质、等量代换即可得;
,再根据直角三角形的性质、等量代换即可得;
(2)先利用正切函数值可得![]() ,再利用相似三角形的判定与性质即可得
,再利用相似三角形的判定与性质即可得![]() ;先根据相似三角形的性质可得
;先根据相似三角形的性质可得![]() ,再根据直角三角形的性质、等量代换即可得;
,再根据直角三角形的性质、等量代换即可得;
(3)先利用直角三角形的性质可得AB、CD的长,再同(2)可得![]() ,
,![]() ,然后分如图3-1和如图3-2(见解析)两种情况,在
,然后分如图3-1和如图3-2(见解析)两种情况,在![]() 中,分别利用勾股定理即可得.
中,分别利用勾股定理即可得.
(1)①![]() ,
,![]()
![]()
![]() 和
和![]() 均为等腰直角三角形
均为等腰直角三角形
![]()
![]()
![]()
在![]() 和
和![]() 中,
中,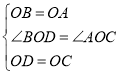
![]()
![]()
即![]()
故答案为:1;
②由①已证:![]()
![]()
![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
![]()
故答案为:![]() ;
;
(2)在![]() 中,
中,![]()
∴![]()
在![]() 中,
中,![]()
∴![]()
∴![]()
![]()
![]() ,即
,即![]()
在![]() 和
和![]() 中,
中,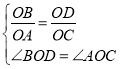
∴![]()
∴![]() ,
,![]()
![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
![]() ;
;
(3)在![]() 中,
中,![]() ,
,![]()
![]()
在![]() 中,
中,![]() ,
,![]()
![]()
同(2)可得:![]() ,
,![]()
设![]() ,则
,则![]()
由题意,分以下两种情况:
①如图3-1,点D在线段AC上
则![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
![]()
②如图3-2,点C在线段AD上
则![]()
在![]() 中,
中,![]() ,即
,即![]()
解得![]() 或
或![]() (不符题意,舍去)
(不符题意,舍去)
![]()
综上,线段![]() 的长为
的长为![]() 或
或![]() .
.



科目:初中数学 来源: 题型:
【题目】已知:![]() 是
是![]() 的内接三角形,且
的内接三角形,且![]() ,直径
,直径![]() 交
交![]() 于点
于点![]() .
.
![]() 如图1 ,求证:
如图1 ,求证:![]() ;
;
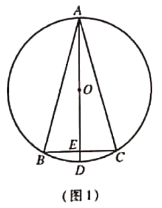
![]() 如图2,将线段
如图2,将线段![]() 绕点
绕点![]() 顺时针旋转得到线段
顺时针旋转得到线段![]() ,旋转角为
,旋转角为![]() 连接
连接![]() 分别交
分别交![]() ,
,![]() 于点
于点![]() ,连接
,连接![]() ,求证:
,求证: ![]() ;
;
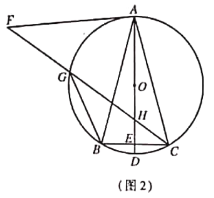
![]() 如图3,在(2)的条件下,当
如图3,在(2)的条件下,当![]() 时,
时,![]() 交
交![]() 于点
于点![]() 若
若![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校随机对本校部分学生进行“假期中,我在家可以这么做:![]() .扎实学习、
.扎实学习、![]() .快乐游戏、
.快乐游戏、![]() .经典阅读、
.经典阅读、![]() .分担劳动、
.分担劳动、![]() .乐享健康”网络调查,并根据调查结果绘制成如下两幅不完整的统计图(若每一位同学只能选择一项),请根据图中信息,回答下列问题.
.乐享健康”网络调查,并根据调查结果绘制成如下两幅不完整的统计图(若每一位同学只能选择一项),请根据图中信息,回答下列问题.

(1)这次调查的总人数是___________人;
(2)请补全条形统计图,并说明扇形统计图中![]() 所对应的圆心角是___________度;
所对应的圆心角是___________度;
(3)若该学校共有学生1700人,则选择![]() 有多少人?
有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】滴滴快车是一种便捷的出行工具,某地的计价规则如表:
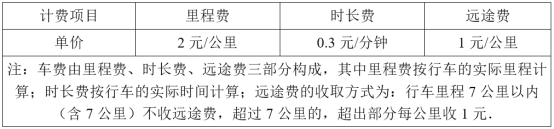
小李与小张分别从不同地点,各自同时乘坐滴滴快车,到同一地点相见,已知到达约定地点时他们的实际行车里程分别为7公里与9公里,两人付给滴滴快车的乘车费相同.其中一人先到达约定地点,他等候另一人的时间等于他自己实际乘车时间,且恰好是另一人实际乘车时间的一半,则小李的乘车费为_____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD与AB相交,连接CO,过点D作⊙O的切线,与AB的延长线交于点E,若DE∥AC,∠BAC=40°,则∠OCD的度数为( )
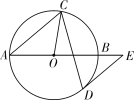
A.65°B.30°C.25°D.20°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求c的值;
(2)当![]() 时,求抛物线顶点的坐标;
时,求抛物线顶点的坐标;
(3)已知点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有两个公共点,结合函数图象,求a的取值范围.
有两个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
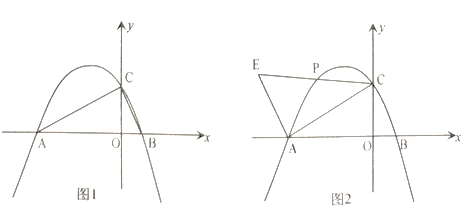
【题目】如图1,已知开口向下的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 不小于
不小于![]() .
.
(1)求点![]() 的坐标(用含
的坐标(用含![]() 的代数式表示);
的代数式表示);
(2)求系数![]() 的取值范围;
的取值范围;
请你根据自身能力从![]() 或(4)小题中任选-题作答.
或(4)小题中任选-题作答.
(3)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 试探究是否存在点
试探究是否存在点![]() ,使得
,使得![]() 的某一个角等于
的某一个角等于![]() 的
的![]() 倍?若存在,求点
倍?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
(4)如图2,当![]() 时,
时,![]() 为直线
为直线![]() 上方抛物线上一动点,过点
上方抛物线上一动点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() 抛物线的对称轴与
抛物线的对称轴与![]() 轴交于点
轴交于点![]() 连接
连接![]() 试探究是否存在点
试探究是否存在点![]() 使得
使得![]() 与
与![]() 相似?若存在,求点
相似?若存在,求点![]() 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com