
【题目】如图,正方形![]() 中,
中,![]() 是
是![]() 上的一点,连接
上的一点,连接![]() ,过
,过![]() 点作
点作![]() ,垂足为点
,垂足为点![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
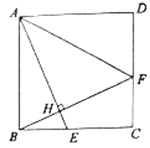
(1)求证:![]() .
.
(2)若正方形边长是5,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】分析: (1)根据ASA证明△ABE≌△BCF,可得结论;
(2)根据(1)得:△ABE≌△BCF,则CF=BE=2,最后利用勾股定理可得AF的长.
详解:
(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABE=∠BCF=90°,
∴∠BAE+∠AEB=90°,
∵BH⊥AE,
∴∠BHE=90°,
∴∠AEB+∠EBH=90°,
∴∠BAE=∠EBH,
在△ABE和△BCF中,

∴△ABE≌△BCF(ASA),
∴AE=BF;
(2)解:∵AB=BC=5,
由(1)得:△ABE≌△BCF,
∴CF=BE=2,
∴DF=5-2=3,
∵四边形ABCD是正方形,
∴AB=AD=5,∠ADF=90°,
由勾股定理得:AF=![]() .
.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】某市民广场地面铺设地砖,决定采用黑白2种地砖,按如下方案铺设,首先在广场中央铺2块黑色砖(如图①),然后在黑色砖的四周铺上白色砖(如图②),再在白色砖的四周铺上黑色砖(如图③),再在黑色砖的四周铺上白色砖(如图④),这样反复更换地砖的颜色,按照这种规律,直至铺满整个广场,观察下图,解决下列问题.
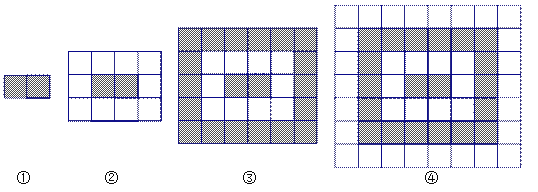
(1)填表
图形序号数 | ① | ② | ③ | ④ | … |
地砖总数(包括黑白地砖) | 2 |
(2)按照这种规律第6个图形一共用去地砖多少块?
(3)按照这种规律第![]() 个图形一共用去地砖多少块?(用含
个图形一共用去地砖多少块?(用含![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知抛物线y=ax2+bx+c的图像经过点A(0,3)、B(1,0),其对称轴为直线l:x=2,过点A作AC∥x轴交抛物线于点C,∠AOB的平分线交线段AC于点E,点P是抛物线上的一个动点,设其横坐标为m.

(1)求抛物线的解析式;
(2)若动点P在直线OE下方的抛物线上,连结PE、PO,当m为何值时,四边形AOPE面积最大,并求出其最大值;
(3)如图②,F是抛物线的对称轴l上的一点,在抛物线上是否存在点P使△POF成为以点P为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春季是传染病多发的季节,积极预防传染病是学校高度重视的一项工作,为此,某校对学生宿舍采取喷洒药物进行消毒.在对某宿舍进行消毒的过程中,先经过![]() 的集中药物喷洒,再封闭宿舍
的集中药物喷洒,再封闭宿舍![]() ,然后打开门窗进行通风,室内每立方米空气中含药量
,然后打开门窗进行通风,室内每立方米空气中含药量![]() 与药物在空气中的持续时间
与药物在空气中的持续时间![]() 之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
之间的函数关系,在打开门窗通风前分别满足两个一次函数,在通风后又成反比例,如图所示.下面四个选项中错误的是( )
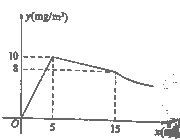
A. 经过![]() 集中喷洒药物,室内空气中的含药量最高达到
集中喷洒药物,室内空气中的含药量最高达到![]()
B. 室内空气中的含药量不低于![]() 的持续时间达到了
的持续时间达到了![]()
C. 当室内空气中的含药量不低于![]() 且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
且持续时间不低于35分钟,才能有效杀灭某种传染病毒.此次消毒完全有效
D. 当室内空气中的含药量低于![]() 时,对人体才是安全的,所以从室内空气中的含药量达到
时,对人体才是安全的,所以从室内空气中的含药量达到![]() 开始,需经过
开始,需经过![]() 后,学生才能进入室内
后,学生才能进入室内
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市在“元旦”期间对顾客实行优惠,规定一次性购物优惠办法:
少于200元,不予优惠;高于200元但低于500元时,九折优惠;消费500元或超过500元时,其中500元部分给予九折优惠,超过500元部分给予八折优惠.根据优惠条件完成下列任务:
(1)王老师一次性购物600元,他实际付款多少元?
(2)若顾客在该超市一次性购物x元,当x小于500但不小于200时,他实际付款0.9x,当x大于或等于500元时,他实际付款多少元?(用含x的代数式表示)
(3)如果王老师两次购物货款合计820元,第一次购物的货款为a元(200<a<300),用含a的式子表示王老师两次购物实际付款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是

A. BC=AC B. CF⊥BF C. BD=DF D. AC=BF
查看答案和解析>>
科目:初中数学 来源: 题型:
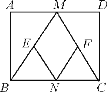
【题目】如图,在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是边BM,CM的中点,当AB与AD满足什么条件时,四边形MENF是正方形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级甲、乙两班分别选5名同学参加“学雷锋见行动”演讲比赛,其预赛成绩如图:
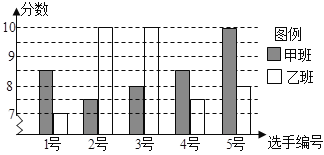
(1)根据上图求出下表中的a,b,c的值(单位:分);
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | a | 8.5 | 0.7 |
乙班 | b | 8 | c | 1.6 |
(2)学校决定在甲、乙两班中选取预赛成绩较好的5人参加该活动的县级演讲比赛,求这5人预赛成绩的平均分数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com