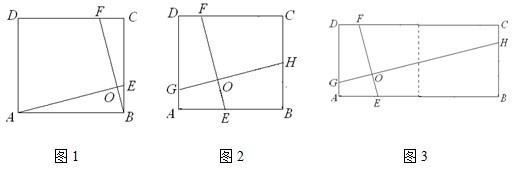
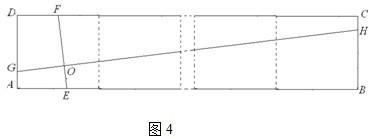
解答:解:(1)延长ED交BC于H,延长GD交PQ于点K,
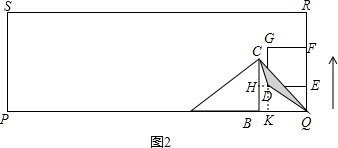
∴EQ=DK=2x,BK=HD=x,BQ=4+x,
∵x=2,BC=6,DE=4,
∴EQ=DK=HB=4,BK=HD=2,BQ=6,
∴CH=2.
在Rt△CHD、Rt△DKQ、Rt△CBQ中,由勾股定理得:
CD=2
,DQ=4
,CQ=6
.
∴CD+DQ=6
,
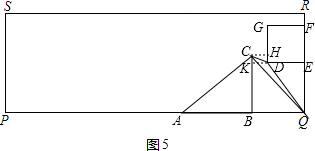
∴CD+DQ=CQ.
故答案为:2
,4
,=;
(2)当0≤x≤2时,如图2,
∵EQ=DK=2x,BK=HD=x,BQ=4+x,CH=6-2x,
∴S
△CDQ=
--,
=-x
2-4x+12
当2<x≤3时,如图5,作CH⊥DG于H,DK⊥BC于K,
∴EQ=BK=2x,CK=HD=6-2x,BQ=4+x,CH=x,
∴S
△CDQ=CK•KD+KB•BQ-
-
-
,
=(6-2x)x+2x(4+x)-
-
-
,
=x
2+4x-12;
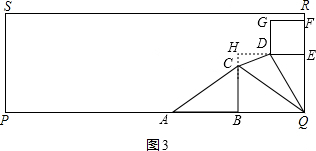
当3<x≤4时,如图3,作DH⊥BC的延长线于H,
∴EQ=HB=2x,HD=x,BQ=4+x,CH=2x-6,
∴S
△CDQ=HB•QB-
-
-
,
=2x(4+x)-
-
-
,
=8x+2x
2-x
2+3x-4x-12-3x,
=x
2+4x-12.
∴S=
| | -x2-4x+12(0≤x≤2) | | x2+4x-12(2<x≤4) |
| |
,
(3)∵纸片DEFG沿RS方向平移,
∴4≤x≤24.
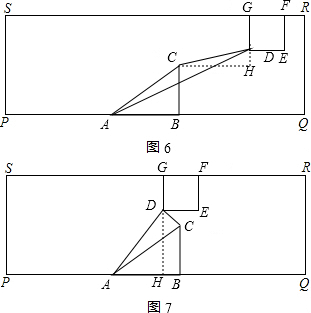
如图6,当CD=AC时,作CH⊥GD的延长线于点H,
∴GR=2x-4,BQ=x+4,
∴DH=12-6-4=2,CH=(x+4)-(2x-4)=8-x,
∵AB=8,BC=6,
∴AC=
=10
在Rt△CHD中,由勾股定理,得
(8-x)
2+2
2=100,
解得:x
1=8+4
,x
2=8-4
<4(舍去);
如图7,当AD=AC时,作DH⊥PQ于点H,
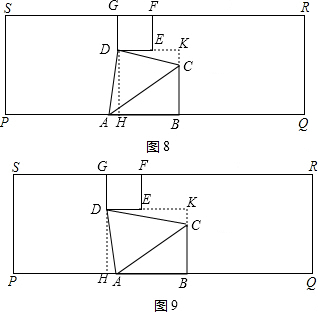
∴GR=2x-4,BQ=x+4,
∴DH=12-4=8,AH=(x+4+8)-(2x-4)=16-x,
在Rt△ADH中,由勾股定理,得
(16-x)
2+8
2=100,
解得:x
1=22,x
2=10;
如图8,当AD=CD时,作DK⊥BC于BC延长线于点K,作DH⊥PQ于点H,
∴GR=2x-4,BQ=x+4,
∴DK=2x-4-(x+4)=x-8,KC=12-4-6=2,
AH=x+4+8-(2x-4)=16-x,DH=12-4=8.
∴(x-8)
2+4=(16-x)
2+64,
∴x=15
;
综上所述:纸片DEFG沿RS方向平移,当x的值为:22,10,15
,8+4
时,
以A、C、D为顶点的三角形是等腰三角形.





 ∴CD+DQ=CQ.
∴CD+DQ=CQ.




 (2013•相城区模拟)如图,在直角梯形ABCD中,∠A=90°; AD∥BC,BC=BD=5cm,CD=
(2013•相城区模拟)如图,在直角梯形ABCD中,∠A=90°; AD∥BC,BC=BD=5cm,CD= 方向行走,经过60次“移位”后,他到达编号为
方向行走,经过60次“移位”后,他到达编号为