
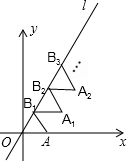
 如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2017的坐标是(2017,2017$\sqrt{3}$).
如图放置的△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,点A在x轴上,点O,B1,B2,B3,…都在正比例函数y=kx的图象l上,则点B2017的坐标是(2017,2017$\sqrt{3}$). 分析 根据等边三角形的性质可得出OB1=B1B2=B2B3=…=2、且直线l的解析式为y=$\sqrt{3}$x,进而可得出点B1、B2、B3、…的坐标,根据坐标的变化即可得出变化规律“Bn(n,$\sqrt{3}$n)”,依此规律即可得出结论.
解答 解:∵△OAB1,△B1A1B2,△B2A2B3,…都是边长为2的等边三角形,
∴OB1=B1B2=B2B3=…=2,且直线l的解析式为y=$\sqrt{3}$x,
∴B1(1,$\sqrt{3}$),B2(2,2$\sqrt{3}$),B3(3,3$\sqrt{3}$),…,
∴Bn(n,$\sqrt{3}$n),
∴B2017(2017,2017$\sqrt{3}$).
故答案为:(2017,2017$\sqrt{3}$).
点评 本题考查了一次函数图象上点的坐标特征、等边三角形的性质以及规律型中点的坐标的变化,根据点的坐标的变化找出变化规律是解题的关键.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:选择题
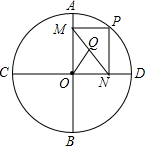 如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,线段OQ所扫过过的面积为( )
如图,⊙O的半径为2,AB,CD是互相垂直的两条直径,点P是⊙O上任意一点(P与A,B,C,D不重合),过点P作PM⊥AB于点M,PN⊥CD于点N,点Q是MN的中点,当点P沿着圆周转过45°时,线段OQ所扫过过的面积为( )| A. | $\frac{π}{4}$ | B. | $\frac{π}{6}$ | C. | $\frac{π}{8}$ | D. | $\frac{π}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
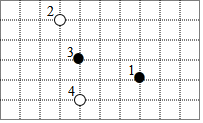 如图所示是围棋棋盘中的一部分,放置在某个平面直角坐标系中,白棋②的坐标是(-3,-1),白棋④的坐标是(-2,-5),则黑棋①的坐标是( )
如图所示是围棋棋盘中的一部分,放置在某个平面直角坐标系中,白棋②的坐标是(-3,-1),白棋④的坐标是(-2,-5),则黑棋①的坐标是( )| A. | (-3,-5) | B. | (0,0) | C. | (1,-4) | D. | (2,-2) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
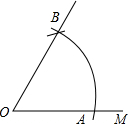 如图,已知射线OM,以O为圆心,以12cm为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则扇形AOB的面积为24πcm2.
如图,已知射线OM,以O为圆心,以12cm为半径画弧,与射线OM交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则扇形AOB的面积为24πcm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 甲 | 乙 | 丙 | 丁 | |
| 平均数(cm) | 175 | 173 | 174 | 175 |
| 方差(cm2) | 3.5 | 3.5 | 12.5 | 13 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com