
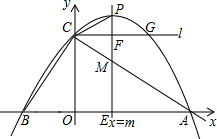
 如图,直线y=2x+4与x轴、y轴相交于B、C两点,抛物线y=ax2-3ax+c过点B、C,且与x轴另一个交点为A,过点C作x轴的平行线l,交抛物线于点G.
如图,直线y=2x+4与x轴、y轴相交于B、C两点,抛物线y=ax2-3ax+c过点B、C,且与x轴另一个交点为A,过点C作x轴的平行线l,交抛物线于点G.分析 (1)首先求出B,C点坐标,进而利用待定系数法求出二次函数解析式,再利用图象上点的坐标性质得出答案;
(2)利用PF分两类:①当0<m<3时,②当m≥3时,分别得出PF的长;
(3)当△PCF与△MEA相似时,P点位置分两种情况:(i)P在G左侧,(ii)P在G右侧,分别得出答案.
解答 解:(1)∵直线y=2x+4与x轴、y轴相交于B、C两点,
∴x=0,y=4;y=0,则x=-2,
故B(-2,0),C(0,4),
将B,C代入y=ax2-3ax+c得:
$\left\{\begin{array}{l}{4a+6a+c=0}\\{c=4}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{2}{5}}\\{c=4}\end{array}\right.$.
∴抛物线的解析式为:$y=-\frac{2}{5}{x^2}+\frac{6}{5}x+4$,
则x=-$\frac{b}{2a}$=$\frac{3}{2}$,
∴A(5,0)、
当y=4,则4=-$\frac{2}{5}$x2+$\frac{6}{5}$x+4,
解得:x1=0,x2=3,
故G(3,4);
(2)∵AC为$y=-\frac{4}{5}x+4$,点M($m\;\;,\;-\frac{4}{5}m+4$),FM=$\frac{4}{5}m$,
∵P(m,$-\frac{2}{5}{m^2}+\frac{6}{5}m+4$),PF分两类:①当0<m<3时,PF=-$\frac{2}{5}$x2+$\frac{6}{5}$x+4-4=$-\frac{2}{5}{m^2}+\frac{6}{5}m$,
②当m≥3时,PF=4-(-$\frac{2}{5}$x2+$\frac{6}{5}$x+4)=$\frac{2}{5}{m^2}-\frac{6}{5}m$;
(3)当△PCF与△MEA相似时,P点位置分两种情况:
(i)P在G左侧,(ii)P在G右侧: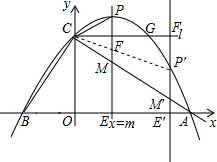
(i)P在G左侧,两个Rt三角形相似有两种情况:①∠PCF=∠MAE;②∠CPF=∠MAE
①∠PCF=∠MAE时,$\frac{PF}{CF}=\frac{ME}{AE}=\frac{OC}{OA}=\frac{4}{5}$,则$\frac{{-\frac{2}{5}{m^2}+\frac{6}{5}m}}{m}=\frac{4}{5}$,
解得:m=1,
②∠CPF=∠MAE时,$\frac{CF}{PF}=\frac{4}{5}$,
解得:m=$-\frac{1}{8}$(舍去)
(ii)P在G右侧,分两种:
①∠PCF=∠MAE时,$\frac{PF}{CF}=\frac{4}{5}$则$\frac{{\frac{2}{5}{m^2}-\frac{6}{5}m}}{m}=\frac{4}{5}$,
解得:m=5(舍去)
②∠CPF=∠MAE时,$\frac{CF}{PF}=\frac{4}{5}$,
解得:m=$\frac{49}{8}$,
综上所述,当以P、C、F为顶点的三角形与△MEA相似时,m=1或 m=$\frac{49}{8}$.
点评 此题主要考查了二次函数综合以及相似三角形的判定与性质等知识,利用分类讨论得出是解题关键,注意不要漏解.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:解答题
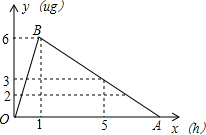 周末小明一家出去游玩,出发前晕车的小明在药店买了晕车药,小明上网查询了这种药的有关数据知道:每升血液中的含药量不低于2μg时这种晕车药才会发挥作用,且这种晕车药服药后每升血液中的含药量y(μg)随着时间x(h)的变化如图所示:
周末小明一家出去游玩,出发前晕车的小明在药店买了晕车药,小明上网查询了这种药的有关数据知道:每升血液中的含药量不低于2μg时这种晕车药才会发挥作用,且这种晕车药服药后每升血液中的含药量y(μg)随着时间x(h)的变化如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com