
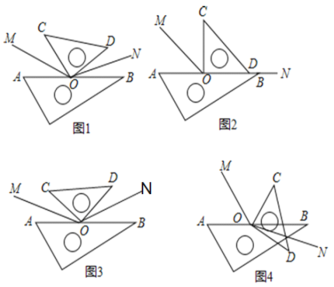
”¾ĢāÄæ”æ×ŪŗĻÓėĢ½¾æĪŹĢā±³¾°ŹżŃ§»ī¶ÆæĪÉĻ£¬ĄĻŹ¦½«Ņ»ø±Čż½Ē³ß°“Ķ¼£Ø1£©ĖłŹ¾Ī»ÖĆ°Ś·Å£¬·Ö±š×÷³ö”ĻAOC£¬”ĻBODµÄĘ½·ÖĻßOM”¢ON£¬Č»ŗóĢį³öČēĻĀĪŹĢā£ŗĒó³ö”ĻMONµÄ¶ČŹż£®
ĢŲĄżĢ½¾æ”°ŠĖȤŠ”×é”±µÄĶ¬Ń§¾ö¶Ø“ÓĢŲĄżČėŹÖĢ½¾æĄĻŹ¦Ģį³öµÄĪŹĢā£¬ĖūĆĒ½«Čż½Ē³ß·Ö±š°“Ķ¼2”¢Ķ¼3ĖłŹ¾µÄ·½Ź½°Ś·Å£¬OMŗĶONČŌČ»ŹĒ”ĻAOCŗĶ”ĻBODµÄ½ĒĘ½·ÖĻߣ®ĘäÖŠ£¬°“Ķ¼2·½Ź½°Ś·ÅŹ±£¬æÉŅŌæ“³ÉŹĒON”¢OD”¢OBŌŚĶ¬Ņ»Ö±ĻßÉĻ£®°“Ķ¼3·½Ź½°Ś·ÅŹ±£¬”ĻAOCŗĶ”ĻBODĻąµČ£®
£Ø1£©ĒėÄć°ļÖś”°ŠĖȤŠ”×é”±½ųŠŠ¼ĘĖć£ŗĶ¼2ÖŠ”ĻMONµÄ¶ČŹżĪŖ”” ”””ć£®Ķ¼3ÖŠ”ĻMONµÄ¶ČŹżĪŖ”” ”””ć£®
·¢ĻÖøŠĪņ
½ā¾öĶźĶ¼2£¬Ķ¼3ĖłŹ¾ĪŹĢāŗ󣬔°ŠĖȤŠ”×é”±ÓÖ¶ŌĶ¼1ĖłŹ¾ĪŹĢā½ųŠŠĮĖĢÖĀŪ£ŗ
Š”Ć÷£ŗÓÉÓŚĶ¼1ÖŠ”ĻAOCŗĶ”ĻBODµÄŗĶĪŖ90”ć£¬ĖłŅŌĪŅĆĒČŻŅ׵Ƶ½”ĻMOCŗĶ”ĻNODµÄŗĶ£¬ÕāŃł¾ĶÄÜĒó³ö”ĻMONµÄ¶ČŹż£®
Š”»Ŗ£ŗÉč”ĻBODĪŖx”ć£¬ĪŅĆĒ¾ĶÄÜÓĆŗ¬xµÄŹ½×Ó·Ö±š±ķŹ¾³ö”ĻNODŗĶ”ĻMOC¶ČŹż£¬ÕāŃłŅ²ÄÜĒó³ö”ĻMONµÄ¶ČŹż£®
£Ø2£©ĒėÄćøł¾ŻĖūĆĒµÄĢø»°ÄŚČŻ£¬Ēó³öĶ¼1ÖŠ”ĻMONµÄ¶ČŹż£®
Ąą±ČĶŲÕ¹
ŹÜµ½”°ŠĖȤŠ”×é”±µÄĘō·¢£¬”°ÖĒ»ŪŠ”×é”±½«Čż½Ē³ß°“Ķ¼4ĖłŹ¾·½Ź½°Ś·Å£¬·Ö±š×÷³ö”ĻAOC”¢”ĻBODµÄĘ½·ÖĻßOM”¢ON£¬ĖūĆĒČĻĪŖŅ²ÄÜĒó³ö”ĻMONµÄ¶ČŹż£®
£Ø3£©ÄćĶ¬Ņā”°ÖĒ»ŪŠ”×é”±µÄæ“·ØĀš£æČōĶ¬Ņā£¬Ēó³ö”ĻMONµÄ¶ČŹż£»Čō²»Ķ¬Ņā£¬ĒėĖµĆ÷ĄķÓÉ£®
”¾“š°ø”æ£Ø1£©135£¬135£»£Ø2£©”ĻMON£½135”ć£»£Ø3£©Ķ¬Ņā£¬”ĻMON£½£Ø90”ć©![]() x”ć£©+x”ć+£Ø45”ć©
x”ć£©+x”ć+£Ø45”ć©![]() x”ć£©£½135”ć.
x”ć£©£½135”ć.
”¾½āĪö”æ
£Ø1£©ÓÉĢāŅāæÉµĆ£¬”ĻMON£½![]() ”Į90”ć+90”ć£¬”ĻMON£½
”Į90”ć+90”ć£¬”ĻMON£½![]() ”ĻAOC+
”ĻAOC+![]() ”ĻBOD+”ĻCOD£¬¼“æÉµĆ³ö“š°ø£»
”ĻBOD+”ĻCOD£¬¼“æÉµĆ³ö“š°ø£»
£Ø2£©øł¾Ż”°OMŗĶONŹĒ”ĻAOCŗĶ”ĻBODµÄ½ĒĘ½·ÖĻß”±æÉĒó³ö”ĻMOC+”ĻNOD£¬ÓÖ”ĻMON£½£Ø”ĻMOC+”ĻNOD£©+”ĻCOD£¬¼“æÉµĆ³ö“š°ø£»
£Ø3£©Éč”ĻBOC£½x”ć£¬Ōņ”ĻAOC£½180”ć©x”ć£¬”ĻBOD£½90”ć©x”ć£¬½ų¶ųĒó³ö”ĻMOCŗĶ”ĻBON£¬ÓÖ”ĻMON£½”ĻMOC+”ĻBOC+”ĻBON£¬¼“æÉµĆ³ö“š°ø.
½ā£ŗ£Ø1£©Ķ¼2ÖŠ”ĻMON£½![]() ”Į90”ć+90”ć£½135”ć£»Ķ¼3ÖŠ”ĻMON£½
”Į90”ć+90”ć£½135”ć£»Ķ¼3ÖŠ”ĻMON£½![]() ”ĻAOC+
”ĻAOC+![]() ”ĻBOD+”ĻCOD£½
”ĻBOD+”ĻCOD£½![]() £Ø”ĻAOC+”ĻBOD£©+90”ć£½
£Ø”ĻAOC+”ĻBOD£©+90”ć£½![]() 90”ć+90”ć£½135”ć£»
90”ć+90”ć£½135”ć£»
¹Ź“š°øĪŖ£ŗ135£¬135£»
£Ø2£©”ß”ĻCOD£½90”ć£¬
”ą”ĻAOC+”ĻBOD£½180”ć©”ĻCOD£½90”ć£¬
”ßOMŗĶONŹĒ”ĻAOCŗĶ”ĻBODµÄ½ĒĘ½·ÖĻߣ¬
”ą”ĻMOC+”ĻNOD£½![]() ”ĻAOC+
”ĻAOC+![]() ”ĻBOD£½
”ĻBOD£½![]() £Ø”ĻAOC+”ĻBOD£©£½45”ć£¬
£Ø”ĻAOC+”ĻBOD£©£½45”ć£¬
”ą”ĻMON£½£Ø”ĻMOC+”ĻNOD£©+”ĻCOD£½45”ć+90”ć£½135”ć£»
£Ø3£©Ķ¬Ņā£¬
Éč”ĻBOC£½x”ć£¬Ōņ”ĻAOC£½180”ć©x”ć£¬”ĻBOD£½90”ć©x”ć£¬
”ßOMŗĶONŹĒ”ĻAOCŗĶ”ĻBODµÄ½ĒĘ½·ÖĻߣ¬
”ą”ĻMOC£½![]() ”ĻAOC£½
”ĻAOC£½![]() £Ø180”ć©x”ć£©£½90”ć©
£Ø180”ć©x”ć£©£½90”ć©![]() x”ć£¬
x”ć£¬
”ĻBON£½![]() ”ĻBOD£½
”ĻBOD£½![]() £Ø90”ć©x”ć£©£½45”ć©
£Ø90”ć©x”ć£©£½45”ć©![]() x”ć£¬
x”ć£¬
”ą”ĻMON£½”ĻMOC+”ĻBOC+”ĻBON£½£Ø90”ć©![]() x”ć£©+x”ć+£Ø45”ć©
x”ć£©+x”ć+£Ø45”ć©![]() x”ć£©£½135”ć£®
x”ć£©£½135”ć£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ A”¢BĮ½µŲĻą¾ą45Ē§Ć×£¬¼×Ęū³µŅŌĆ抔Ź±50Ē§Ć×µÄĖŁ¶Č“ÓAµŲ³ö·¢£¬ŅŅĘū³µŅŌĆ抔Ź±40Ē§Ć×µÄĖŁ¶Č“ÓBµŲ³ö·¢
£Ø1£©ČōĮ½³µĶ¬Ź±³ö·¢£¬ĻąĻņ¶ųŠŠ£¬ĪŹ¾¹ż¼øŠ”Ź±£¬Į½³µĻą¾ą30Ē§Ć×£æ
£Ø2£©ČōĮ½³µĶ¬Ź±³ö·¢£¬Ķ¬Ļņ¶ųŠŠ£¬ĪŹ¾¹ż¼øŠ”Ź±£¬Į½³µĻą¾ą30Ē§Ć×£æ
£Ø3£©ČōŅŅ³µĻČ³ö·¢°ėŠ”Ź±,Ķ¬Ļņ¶ųŠŠ,Ōņ¾¹ż¼øŠ”Ź±£¬Į½³µĻą¾ą30Ē§Ć×£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
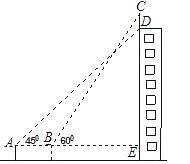
”¾ĢāÄæ”æČēĶ¼£¬Ä³“±“óĀ„¶„²æÓŠŅ»æé¹ćøęÅĘCD£¬¼×”¢ŅŅĮ½ČĖ·Ö±šŌŚA”¢BĮ½“¦£¬¼×²āµĆµćDµÄŃö½ĒĪŖ45”ć£¬ŅŅ²āµĆµćCµÄŃö½ĒĪŖ60”ć£¬ŅŃÖŖĮ½ČĖŹ¹ÓĆµÄ²ā½ĒŅĒµÄø߶ČAF”¢BGĻąµČ£¬ĒŅA”¢B”¢EČżµćŌŚŅ»ĢõÖ±ĻßÉĻ£¬AB=8m£¬BE=15m£®Ēó¹ćøęÅĘCDµÄøߣؾ«Č·µ½1m£©£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æ¼×”¢ŅŅĮ½¼ŅÉĢ³”ŅŌĶ¬ŃłµÄ¼Ūøń³öŹŪĶ¬ŃłµÄµēĘ÷£¬µ«ø÷×ŌĶĘ³öµÄÓÅ»Ż·½°ø²»Ķ¬£®¼×ÉĢ³”¹ę¶Ø£ŗ·²³¬¹ż ![]() ŌŖµÄµēĘ÷£¬³¬³öµÄ½š¶ī°“
ŌŖµÄµēĘ÷£¬³¬³öµÄ½š¶ī°“ ![]() ŹÕČ”£»ŅŅÉĢ³”¹ę¶Ø£ŗ·²³¬¹ż
ŹÕČ”£»ŅŅÉĢ³”¹ę¶Ø£ŗ·²³¬¹ż ![]() ŌŖµÄµēĘ÷£¬³¬³öµÄ½š¶ī°“
ŌŖµÄµēĘ÷£¬³¬³öµÄ½š¶ī°“ ![]() ŹÕČ”£®Ä³¹ĖæĶ¹ŗĀņµÄµēĘ÷¼ŪøńŹĒ
ŹÕČ”£®Ä³¹ĖæĶ¹ŗĀņµÄµēĘ÷¼ŪøńŹĒ ![]() ŌŖ£®
ŌŖ£®
£Ø1£©µ± ![]() Ź±£¬øĆ¹ĖæĶӦєŌńŌŚ ÉĢ³”¹ŗĀņ±Č½ĻŗĻĖć£»
Ź±£¬øĆ¹ĖæĶӦєŌńŌŚ ÉĢ³”¹ŗĀņ±Č½ĻŗĻĖć£»
£Ø2£©µ± ![]() Ź±£¬·Ö±šÓĆ“śŹżŹ½±ķŹ¾ŌŚĮ½¼ŅÉĢ³”¹ŗĀņµēĘ÷ĖłŠčø¶µÄ·ŃÓĆ£»
Ź±£¬·Ö±šÓĆ“śŹżŹ½±ķŹ¾ŌŚĮ½¼ŅÉĢ³”¹ŗĀņµēĘ÷ĖłŠčø¶µÄ·ŃÓĆ£»
£Ø3£©µ± ![]() Ź±£¬øĆ¹ĖæĶӦєŌńÄÄŅ»¼ŅÉĢ³”¹ŗĀņ±Č½ĻŗĻĖć?ĖµĆ÷ĄķÓÉ£®
Ź±£¬øĆ¹ĖæĶӦєŌńÄÄŅ»¼ŅÉĢ³”¹ŗĀņ±Č½ĻŗĻĖć?ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŹĢā£ŗČēŗĪæģĖŁ¼ĘĖć1+2+3+”+n µÄÖµÄŲ£æ
£Ø1£©Ģ½¾æ£ŗĮīs=1+2+3+”+n¢Ł£¬Ōņs=n+n-1+”+2+1¢Ś
¢Ł+¢ŚµĆ2s=(n+1)(n+1)+”+(n+1)=n![]() (n+1)
(n+1)
Ņņ“Ė![]() _________________.
_________________.
(2)Ó¦ÓĆ£ŗ
¢Ł¼ĘĖć£ŗ![]() ________£»
________£»
¢ŚČēĶ¼1£¬Ņ»“®Į¬ŠųµÄÕūŹż1£¬2£¬3£¬4£¬”£¬×ŌÉĻĶłĻĀÅÅĮŠ£¬×īÉĻĆęŅ»ŠŠÓŠŅ»øöŹż£¬ŅŌĻĀø÷ŠŠ¾ł±ČÉĻŅ»ŠŠ¶ąŅ»øöŹż×Ö£¬Čō¹²ÓŠ15ŠŠŹż×Ö£¬Ōņ×īµ×ĻĀŅ»ŠŠ×ī×ó±ßµÄŹżŹĒ_______£»

¢ŪČēĶ¼2£¬Ņ»“®Į¬ŠųµÄÕūŹż-25£¬-24£¬-23£¬”£¬°“Ķ¼1·½Ź½ÅÅĮŠ£¬¹²ÓŠ14ŠŠŹż×Ö£¬ĒóĶ¼2ÖŠĖłÓŠŹż×ÖµÄŗĶ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŹŠĒų×Ō2014Äź1ŌĀĘš£¬¾ÓĆńÉś»īÓĆĖ®æŖŹ¼ŹµŠŠ½×ĢŻŹ½¼ĘĮæĖ®¼Ū£¬øĆ½×ĢŻŹ½¼ĘĮæĖ®¼Ū·ÖĪŖČż¼¶£ØČēĻĀ±ķĖłŹ¾£©£ŗ
ŌĀÓĆĖ®Įæ£Ø¶Ö£© | Ė®¼Ū£ØŌŖ/¶Ö£© |
µŚŅ»¼¶ 20¶ÖŅŌĻĀ£Øŗ¬20¶Ö£© | 1£®6 |
µŚ¶ž¼¶ 20¶Ö©30¶Ö£Øŗ¬30¶Ö£© | 2£®4 |
µŚČż¼¶ 30¶ÖŅŌÉĻ | 3£®2 |
Ąż£ŗijÓĆ»§µÄŌĀÓĆĖ®ĮæĪŖ32¶Ö£¬°“Čż¼¶¼ĘĮæÓ¦½ÉĖ®·ŃĪŖ£ŗ
1£®6”Į20£«2£®4”Į10£«3£®2”Į2£½62£®4£ØŌŖ£©
£Ø1£©Čē¹ū¼×ÓĆ»§µÄŌĀÓĆĖ®ĮæĪŖ12¶Ö£¬Ōņ¼×Šč½ÉµÄĖ®·ŃĪŖ ŌŖ£»
£Ø2£©Čē¹ūŅŅÓĆ»§½ÉµÄĖ®·ŃĪŖ39£®2ŌŖ£¬ŌņŅŅŌĀÓĆĖ®Įæ ¶Ö£»
£Ø3£©Čē¹ū±ūÓĆ»§µÄŌĀÓĆĖ®ĮæĪŖa¶Ö£¬Ōņ±ūÓĆ»§øĆŌĀÓ¦½ÉĖ®·Ń¶ąÉŁŌŖ£æ£ØÓĆŗ¬aµÄ“śŹżŹ½±ķŹ¾£¬²¢»Æ¼ņ£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŅ»“ĪŗÆŹż![]() µÄĶ¼ĻóÓė·“±ČĄżŗÆŹż
µÄĶ¼ĻóÓė·“±ČĄżŗÆŹż![]() µŚŅ»ĻóĻŽÄŚµÄĶ¼ĻóĻą½»ÓŚµć
µŚŅ»ĻóĻŽÄŚµÄĶ¼ĻóĻą½»ÓŚµć![]() £¬Óė
£¬Óė![]() ÖįĻą½»ÓŚµć
ÖįĻą½»ÓŚµć![]() .
.
(1)Ēó![]() ŗĶ
ŗĶ![]() µÄÖµ£»
掙术
(2)¹Ū²ģ·“±ČĄżŗÆŹż![]() µÄĶ¼Ļ󣬵±
µÄĶ¼Ļ󣬵±![]() Ź±£¬ĒėÖ±½ÓŠ“³ö
Ź±£¬ĒėÖ±½ÓŠ“³ö![]() µÄȔֵ·¶Ī§£»
µÄȔֵ·¶Ī§£»
(3)ČēĶ¼£¬ŅŌ![]() ĪŖ±ß×÷ĮāŠĪ
ĪŖ±ß×÷ĮāŠĪ![]() £¬Ź¹µć
£¬Ź¹µć![]() ŌŚ
ŌŚ![]() ÖįÕż°ėÖįÉĻ£¬µć
ÖįÕż°ėÖįÉĻ£¬µć![]() ŌŚµŚŅ»ĻóĻŽ£¬Ė«ĒśĻß½»
ŌŚµŚŅ»ĻóĻŽ£¬Ė«ĒśĻß½»![]() ÓŚµć
ÓŚµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ”¢
”¢![]() £¬Ēó
£¬Ēó![]() .
.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
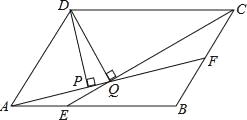
”¾ĢāÄæ”æČēĶ¼£¬Ę½ŠŠĖıߊĪABCDÖŠ£¬AB£ŗBC£½3£ŗ2£¬”ĻDAB£½60”ć£¬EŌŚABÉĻ£¬Čē¹ūAE£ŗEB£½1£ŗ2£¬FŹĒBCµÄÖŠµć£¬¹żD·Ö±š×÷DP”ĶAFÓŚP£¬DQ”ĶCEÓŚQ£¬ÄĒĆ“DP£ŗDCµČÓŚ_____£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijĀĆÓĪ¾°µćµÄÄźÓĪæĶĮæy£ØĶņČĖ£©ŹĒĆÅʱ¼Ūøńx£ØŌŖ£©µÄŅ»“ĪŗÆŹż£¬ĘäŗÆŹżĶ¼ĻńČēĻĀĶ¼£®

£Ø1£©Ēóy¹ŲÓŚxµÄŗÆŹż½āĪöŹ½£»
£Ø2£©¾¹ż¾°µć¹¤×÷ČĖŌ±Ķ³¼Ę·¢ĻÖ£ŗĆæĀō³öŅ»ÕÅĆÅʱĖłŠč³É±¾ĪŖ20ŌŖ£®ÄĒĆ“ŅŖĻė»ńµĆÄźĄūČó11500ĶņŌŖ£¬ĒŅĆÅʱ¼Ūøń²»µĆøßÓŚ230ŌŖ£¬øĆÄźµÄĆÅʱ¼ŪøńÓ¦øƶØĪŖ¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com