
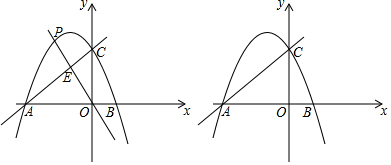
���� ��1������õ�A�͵�C�����꣬Ȼ��A��C��O������ֱ���������ߵĽ���ʽ�ɵõ�����a��b��c�ķ����飬�Ӷ������a��b��c��ֵ��
��2�����ȸ��ݹ��ɶ����ã�AC=4$\sqrt{2}$����S��AOE��S��OCE=3��1�ɵõ�AE=3$\sqrt{2}$����AE=6$\sqrt{2}$��Ȼ�����E��EH��x�ᣬ����ΪH��Ȼ�����OH��EH�ij����Ӷ�����õ�E�����꣬����E���������y=kx�����k��ֵ�������E������Ϊ��x��x+4������AE=$\sqrt{��x+4��^{2}+��x+4��^{2}}$��OE=$\sqrt{{x}^{2}+��x+4��^{2}}$��Ȼ���ΪAO=OE��AO=AE��EA=EO��������з�����⼴�ɣ�
��� �⣺��1����x=0����y=x+4��y=4��
���C��������0��4����
��y=0����y+x+4�ã�x=-4��
���A��������-4��0����
��������y=-$\frac{1}{2}$x2+bx+c������A�͵�C���ã�$\left\{\begin{array}{l}{-\frac{1}{2}����-4��^{2}-4b+c=0}\\{c=4}\end{array}\right.$��
��ã�h=-1��c=4��
�������ߵĽ���ʽΪy=-$\frac{1}{2}$x2-x+4��
��2���١�OA=OC=4�����ݹ��ɶ����ã�AC=4$\sqrt{2}$��
��S��AOE��S��OCE=3��1ʱ��
��AE��EC=3��1��
����E���߶�AC��ʱ������E��EH��x�ᣬ����ΪH����AE=3$\sqrt{2}$��CE=$\sqrt{2}$��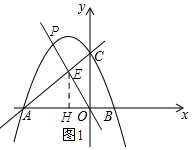
��OH=1��EH=3��
���E��������-1��3����
�ѵ�E���������y=kx�ã�k=-3��
�������������Ľ���ʽΪy=-3x��
����E���߶�AC�ij�����ʱ������E��EH��x�ᣬ����ΪH����AE=6$\sqrt{2}$��EC=2$\sqrt{2}$��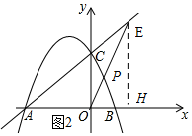
��OH=2��HE=6��
���E��������2��6����
�ѵ�E��2��6������y=kx�ã�k=3��
��������k��ֵΪ3��-3��
�����E��������x��x+4������AE=$\sqrt{��x+4��^{2}+��x+4��^{2}}$��OE=$\sqrt{{x}^{2}+��x+4��^{2}}$��
��AO=OEʱ��$\sqrt{{x}^{2}+��x+4��^{2}}$=4�������ã�2x2+8x=0�����x=0��x=-4����ȥ����
���E��������0��4����
��AO=AEʱ��$\sqrt{��x+4��^{2}+��x+4��^{2}}$=4�������ã�x2+8x+8=0����ã�x=-4+2$\sqrt{2}$��x=-4-2$\sqrt{2}$��
���E��������2$\sqrt{2}$-4��2$\sqrt{2}$����-2$\sqrt{2}$-4��-2$\sqrt{2}$����
��EA=EOʱ��$\sqrt{��x+4��^{2}+��x+4��^{2}}$=$\sqrt{{x}^{2}+��x+4��^{2}}$�������ã�8x+16=0����ã�x=-2��
���E��������-2��2����
��E��������-2��2����0��4����2$\sqrt{2}$-4��2$\sqrt{2}$����-2$\sqrt{2}$-4��-2$\sqrt{2}$����
���� ������Ҫ������Ƕ��κ������ۺ�Ӧ�ã��������ҪӦ���˶��κ��������ʡ������ε������ʽ�����������εĶ��塢����ľ��빫ʽ�����ݵ��������εĶ����Լ������ľ��빫ʽ�г������ǽ����Ĺؼ���


 ϰ�⾫ѡϵ�д�
ϰ�⾫ѡϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��Rt��ABC�У���ACB=90�㣬��A=50�㣬�����۵���ʹ��A���ڱ�CB��A�䴦���ۺ�ΪCD�����A��DB�Ķ���Ϊ10�㣮
��ͼ��Rt��ABC�У���ACB=90�㣬��A=50�㣬�����۵���ʹ��A���ڱ�CB��A�䴦���ۺ�ΪCD�����A��DB�Ķ���Ϊ10�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
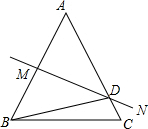 ��ͼ���ڡ�ABC�У�AB=AC����AB�Ĵ�ֱƽ����MN��AC�ڵ�D������BCD���ܳ�Ϊ24cm��BC=10cm����AB�ij�Ϊ14cm��
��ͼ���ڡ�ABC�У�AB=AC����AB�Ĵ�ֱƽ����MN��AC�ڵ�D������BCD���ܳ�Ϊ24cm��BC=10cm����AB�ij�Ϊ14cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
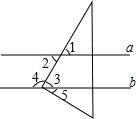 ��ͼ����ֱ֪��a��b���ֽ�һֱ�����ǰ��ֱ�Ƕ������ֱ��b�ϣ�����3=50�㣬�����н��۴�����ǣ�������
��ͼ����ֱ֪��a��b���ֽ�һֱ�����ǰ��ֱ�Ƕ������ֱ��b�ϣ�����3=50�㣬�����н��۴�����ǣ�������| A�� | ��1=50�� | B�� | ��2=50�� | C�� | ��4=130�� | D�� | ��5=30�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com