
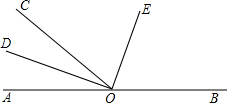
 如图,点O为直线AB上的一点,∠BOC=130°,OE平分∠BOC,DO⊥OE.
如图,点O为直线AB上的一点,∠BOC=130°,OE平分∠BOC,DO⊥OE.分析 (1)直接利用小于平角的定义分析得出答案;
(2)直接利用角平分线的定义结合已知得出答案;
(3)利用角平分线的定义分别得出∠AOD和∠DOC的度数,进而得出答案.
解答 解:(1)图中小于平角的角有:∠AOD,∠AOC,∠AOE,∠DOC,∠DOE,∠DOB,∠COE,∠COB,∠EOB,共9个;
故答案为:9;
(2)∵OE平分∠BOC,∠BOC=130°,
∴∠BOE=$\frac{1}{2}$∠BOC=65°,
∴∠AOE=180°-∠BOE=115°;
(3)∵OE平分∠BOC,∠BOC=130°,
∴∠COE=$\frac{1}{2}$∠BOC=65°,
∵OD⊥OE,
∴∠DOE=90°,
∴∠DOC=∠DOE-∠COE=90°-65°=25°,
∵∠AOD=∠AOE-∠DOE=115°-90°=25°,
∴∠AOD=∠DOC,
即OD平分∠AOC.
点评 此题主要考查了角平分线的定义以及垂线的定义,正确把握相关定义是解题关键.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:选择题
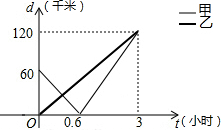 甲、乙两船沿直线航道AC匀速航行,甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行,设t小时后甲、乙两船与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,下列说法:①乙船的速度是40千米/时;②甲船航行1小时到达B处;③甲、乙两船航行0.6小时相遇;④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的个数是( )
甲、乙两船沿直线航道AC匀速航行,甲船从起点A出发,同时乙船从航道AC中途的点B出发,向终点C航行,设t小时后甲、乙两船与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,下列说法:①乙船的速度是40千米/时;②甲船航行1小时到达B处;③甲、乙两船航行0.6小时相遇;④甲、乙两船的距离不小于10千米的时间段是0≤t≤2.5.其中正确的说法的个数是( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
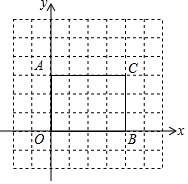 如图所示,矩形AOBC各点的坐标分别为A(0,3),O(0,0),B(4,0),C(4,3).以原点O为位似中心,将这个矩形缩小为原来的$\frac{1}{2}$,写出新矩形A′O′B′C′各顶点的坐标并画出图形(只要画出一个).
如图所示,矩形AOBC各点的坐标分别为A(0,3),O(0,0),B(4,0),C(4,3).以原点O为位似中心,将这个矩形缩小为原来的$\frac{1}{2}$,写出新矩形A′O′B′C′各顶点的坐标并画出图形(只要画出一个).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
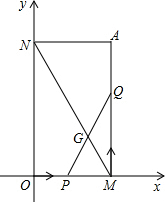 如图,已知过点A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.设PQ与MN交于点G.
如图,已知过点A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点.设PQ与MN交于点G.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 直线AB是平角 | B. | 凡是直角都相等 | ||
| C. | 两个锐角的和一定是钝角 | D. | 若AM=$\frac{1}{2}$AB,则点M是线段AB的中点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com