(2012•聊城一模)在一平直河岸l同侧有A,B两个村庄,A,B到l的距离分别是3km和2km,AB=akm(a>1).现计划在河岸l上建一抽水站P,用输水管向两个村庄供水.
某班数学兴趣小组设计了两种铺设管道方案:图1是方案一的示意图,设该方案中管道长度为d
1,且d
1=PB+BA(km)(其中BP⊥l于点P);图2是方案二的示意图,设该方案中管道长度为d
2,且d
2=PA+PB(km)(其中点A′与点A关于l对称,A′B与l交于点P).
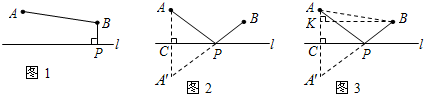
观察计算:(1)在方案一中,d
1=
a+2
a+2
km(用含a的式子表示);
(2)在方案二中,组长小宇为了计算d
2的长,作了如图3所示的辅助线,请你按小宇同学的思路计算,d
2=
km(用含a的式子表示).
探索归纳:(1)①当a=4时,比较大小:d
1<
<
d
2(填“>”、“=”或“<”);
②当a=6时,比较大小:d
1>
>
d
2(填“>”、“=”或“<”);
(2)请你参考方法指导,就a(当a>1时)的所有取值情况进行分析,要使铺设的管道长度较短,应选择方案一还是方案二?
方法指导:当不易直接比较两个正数m与n的大小时,可以对它们的平方进行比较:
∵m
2-n
2=(m+n)(m-n),m+n>0,
∴(m
2-n
2)与(m-n)的符号相同.
当m
2-n
2>0时,m-n>0,即m>n;
当m
2-n
2=0时,m-n=0,即m=n;
当m
2-n
2<0时,m-n<0,即m<n.

