【答案】
分析:(1)已知直线L过A,B两点,可将两点的坐标代入直线的解析式中,用待定系数法求出直线L的解析式;
(2)求三角形OPQ的面积,就需知道底边OP和高QM的长,已知了OP为t,关键是求出QM的长.已知了QM垂直平分OP,那么OM=

t,然后要分情况讨论:
①当OM<OB时,即0<t<2时,BM=OB-OM,然后在等腰直角三角形BQM中,即可得出QM=BM,由此可根据三角形的面积公式得出S与t的函数关系式.
②当OM>OB时,即当t≥2时,BM=OM-OB,然后根据①的方法即可得出S与t的函数关系式.
然后可根据0<t<2时的函数的性质求出S的最大值;
(3)如果存在这样的点C,那么CQ=QP=OQ,因此C,O就关于直线BL对称,因此C的坐标应该是(1,1).那么只需证明CQ⊥PQ即可.分三种情况进行讨论.
①当Q在线段AB上(Q,B不重合),且P在线段OB上时.要证∠CQP=90°,那么在四边形CQPB中,就需先证出∠QCB与∠QPB互补,由于∠QPB与∠QPO互补,而∠QPO=∠QOP,因此只需证∠QCB=∠QOB即可,根据折叠的性质,这两个角相等,由此可得证.
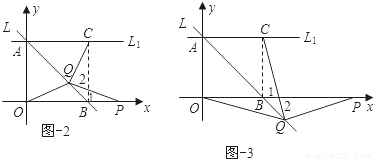
②当Q在线段AB上,P在OB的延长线上时,根据①已得出∠QPB=∠QCB,那么这两个角都加上一个相等的对顶角后即可得出∠CQP=∠CBP=90度.
③当Q与B重合时,很显然,三角形CQP应该是个等腰直角三角形.
综上所述即可得出符合条件C点的坐标.
解答:解:由题意得
(1)y=1-x;
(2)∵OP=t,
∴Q点的横坐标为

,
①当
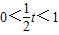
,即0<t<2时,
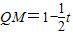
,
∴S
△OPQ=

t(1-

t).
②当t≥2时,QM=|1-

t|=

t-1,
∴S
△OPQ=

t(

t-1).
∴
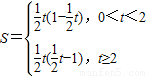
当0<

t<1,即0<t<2时,S=

t(1-

t)=-

(t-1)
2+

,
∴当t=1时,S有最大值

;
(3)由OA=OB=1,
所以△OAB是等腰直角三角形,
若在L
1上存在点C,使得△CPQ是以Q为直角顶点的等腰直角三角形,
则PQ=QC,
所以OQ=QC,又L
1∥x轴,则C,O两点关于直线L对称,
所以AC=OA=1,得C(1,1).下面证∠PQC=90度.连CB,则四边形OACB是正方形.
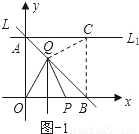
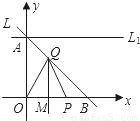
①当点P在线段OB上,Q在线段AB上(Q与B、C不重合)时,如图-1.
由对称性,得∠BCQ=∠QOP,∠QPO=∠QOP,
∴∠QPB+∠QCB=∠QPB+∠QPO=180°,
∴∠PQC=360°-(∠QPB+∠QCB+∠PBC)=90度.
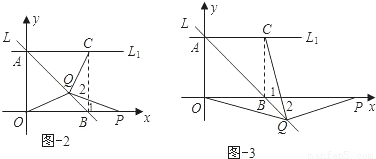
②当点P在线段OB的延长线上,Q在线段AB上时,如图-2,如图-3
∵∠QPB=∠QCB,∠1=∠2,
∴∠PQC=∠PBC=90度.
③当点Q与点B重合时,显然∠PQC=90度.
综合①②③,∠PQC=90度.
∴在L
1上存在点C(1,1),使得△CPQ是以Q为直角顶点的等腰直角三角形.
点评:本题结合了三角形的相关知识考查了一次函数及二次函数的应用,要注意的是(2)中为保证线段的长度不为负数要分情况进行求解.(3)中由于Q,P点的位置不确定,因此要分类进行讨论不要漏解.

 t,然后要分情况讨论:
t,然后要分情况讨论:

 ,
,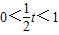 ,即0<t<2时,
,即0<t<2时,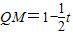 ,
, t(1-
t(1- t).
t). t|=
t|= t-1,
t-1, t(
t( t-1).
t-1).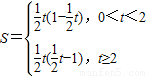
 t<1,即0<t<2时,S=
t<1,即0<t<2时,S= t(1-
t(1- t)=-
t)=- (t-1)2+
(t-1)2+ ,
, ;
;


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案 三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由.
三角形?若存在,求出点C的坐标,并证明;若不存在,请说明理由. 平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式.
平移,设平移过程中△F′O′G′与四边形ODCE重叠部分面积为y,OO′的长为x(0≤x≤1),求y与x的函数关系式. 如图所示:已知直线y=
如图所示:已知直线y=