
【题目】如图,已知四边形ABCD中,∠ABC=90°,∠ADC=90°,AB=6,CD=4,BC的延长线与AD的延长线交于点E.
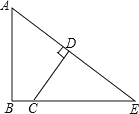
(1)若∠A=60°,求BC的长;
(2)若sinA=![]() ,求AD的长.
,求AD的长.
(注意:本题中的计算过程和结果均保留根号)
【答案】(1)6![]() ﹣8;(2)
﹣8;(2)![]() .
.
【解析】
试题分析:(1)根据锐角三角函数求得BE和CE的长,根据BC=BE﹣CE即可求得BC的长;(2)根据题意求得AE和DE的长,由AD=AE﹣DE即可求得AD的长.
试题解析:(1)∵∠A=60°,∠ABE=90°,AB=6,tanA=![]() ,
,
∴∠E=30°,BE=tan60°6=6![]() ,
,
又∵∠CDE=90°,CD=4,sinE=![]() ,∠E=30°,
,∠E=30°,
∴CE=![]() =8,
=8,
∴BC=BE﹣CE=6![]() ﹣8;
﹣8;
(2))∵∠ABE=90°,AB=6,sinA=![]() =
=![]() ,
,
∴设BE=4x,则AE=5x,得AB=3x,
∴3x=6,得x=2,
∴BE=8,AE=10,
∴tanE=![]() =
=![]() =
=![]() =
=![]() ,
,
解得,DE=![]() ,
,
∴AD=AE﹣DE=10﹣![]() =
=![]() ,
,
即AD的长是![]() .
.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
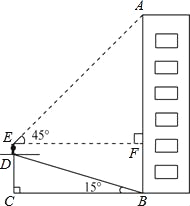
【题目】小华为了测量楼房AB的高度,他从楼底的B处沿着斜坡向上行走20m,到达坡顶D处.已知斜坡的坡角为15°.小华的身高ED是1.6m,他站在坡顶看楼顶A处的仰角为45°,求楼房AB的高度.(计算结果精确到1m)(参考数据:sin15°=![]() ,cos15°=
,cos15°=![]() ,tan15°=
,tan15°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
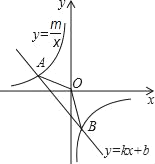
【题目】如图,已知A(4,2)、B(n,﹣4)是一次函数y=kx+b图象与反比例函数![]() 图象的两个交点.
图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)直接写出△AOB的面积;
(3)根据图象直接写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,以AB为直径的⊙O与AC边交于点D,过点D的直线交BC边于点E,∠BDE=∠A.
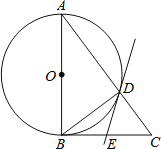
(1)判断直线DE与⊙O的位置关系,并说明理由.
(2)若⊙O的半径R=5,tanA=![]() ,求线段CD的长.
,求线段CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1,W2(单位:元)
(1)用含x的代数式分别表示W1,W2;
(2)当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(12,0),B(0,9)分别是平面直解坐标系xOy坐标轴上的点,经过点O且与AB相切的动圆与x轴、y轴分别相交与点P、Q,则线段PQ长度的最小值是( )
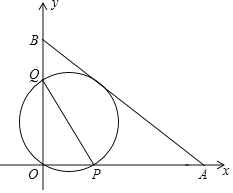
A.![]() B.10C.7.2D.
B.10C.7.2D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com