
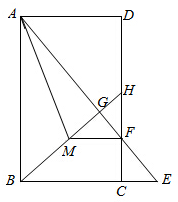
 如图所示,在矩形ABCD中,点E是边BC延长线上一点,连结AE,交DC于点F,作BH⊥AE于点G,交DC于点H,作FM∥BC交BH于点M,连结AM.且FH=FE.AD=2$\sqrt{7}$.AG=6.
如图所示,在矩形ABCD中,点E是边BC延长线上一点,连结AE,交DC于点F,作BH⊥AE于点G,交DC于点H,作FM∥BC交BH于点M,连结AM.且FH=FE.AD=2$\sqrt{7}$.AG=6.分析 (1)由条件可证得△HFG≌△EFC,可得GH=CE,CF=GF,进一步可证得BH=BE,则有BG=BC,在Rt△ABG中可求得AB,又可证明△ADF≌△BGA,则AF=AB,可求得AF的长;
(2)利用(1)中的结论可求得DF,CF,又△CEF∽△DAF,可求得CE的长,可求得可△ABE的面积,则S四边形AGHD=S矩形ABCD-S四边形ABCF-S△GHF,利用全等S△GHF=S△CEF,则可求得四边形AGHD的面积;
(3)延长FM交AB于点N,由(2)中求得DF的长,则可求得AN的长,可求得AN=AG,可证明△AGM≌△ANM,可得∠BAG=2∠BAM,在Rt△ABG中,由直角三角形的性质可得∠BAG=90°-∠HBA,可证得结论.
解答 (1)解:
∵四边形ABCD为矩形,
∴AB=CD,AD=BC=2$\sqrt{7}$,∠D=∠FCE=90°
∵BH⊥AE,
∴∠HGF=∠AGB=90°
在△HFG和△EFC中
$\left\{\begin{array}{l}{∠HGF=∠ECF}\\{∠HFG=∠EFC}\\{HF=EF}\end{array}\right.$
∴△HFG≌△EFC(AAS),
∴GF=CF,
∴HF+CF=GF+EF即CH=GE,
在△BCH和△BGE中
$\left\{\begin{array}{l}{∠HBC=∠GBE}\\{∠BCH=∠BGE}\\{CH=GE}\end{array}\right.$
∴△BCH≌△BGE(AAS),
∴BG=BC=AD=2$\sqrt{7}$,
在R△ABG中,AG=6,则由勾股定理可得AB=$\sqrt{A{G}^{2}+B{G}^{2}}$=$\sqrt{{6}^{2}+(2\sqrt{7})^{2}}$=8,
∵AB∥CD,
∴∠BAG=∠AFD,
在△ABG和△FDA中
$\left\{\begin{array}{l}{∠AGB=∠ADF}\\{∠BAG=∠DFA}\\{BG=AD}\end{array}\right.$
∴△ABG≌△FDA(AAS),
∴AF=AB=8;
(2)解:
由(1)可知△ABG≌△FDA,
∴DF=AG=6,
∴CF=CD-DF=AB-DF=8-6=2,
∵BE∥AD,
∴△CEF∽△DAF,
∴$\frac{CE}{AD}$=$\frac{CF}{DF}$,即$\frac{CE}{2\sqrt{7}}$=$\frac{2}{6}$,
∴CE=$\frac{2\sqrt{7}}{3}$,则BE=BC+CE=AD+CE=2$\sqrt{7}$+$\frac{2\sqrt{7}}{3}$=$\frac{8\sqrt{7}}{3}$,
∴S△ABE=$\frac{1}{2}$AB•BE=$\frac{1}{2}$×8×$\frac{8\sqrt{7}}{3}$=$\frac{32\sqrt{7}}{3}$,
∵△HGF≌△CEF,
∴S△GHF=S△CEF,且S矩形ABCD=AB•BC=8×2$\sqrt{7}$=16$\sqrt{7}$,
∴S四边形AGHD=S矩形ABCD-S四边形ABCF-S△GHF=S矩形ABCD-(S四边形ABCF+S△GHF)=S矩形ABCD-S△ABE=16$\sqrt{7}$-$\frac{32\sqrt{7}}{3}$=$\frac{16\sqrt{7}}{3}$;
(3)证明:
如图,延长FM交AB于点N,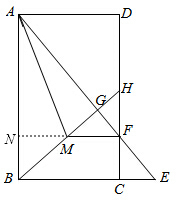
∵MF∥BC,
∴四边形BCFN为矩形,
∴NB=FC=2,则AN=8-2=6=AG,
在△AMN和△AMG中
$\left\{\begin{array}{l}{AN=AG}\\{∠ANM=∠AGM}\\{AM=AM}\end{array}\right.$
∴△AMG≌△AMG(SAS),
∴∠BAM=∠GAM,
∴∠BAG=2∠BAM,
在Rt△ABG中,∠BAG=90°-∠HBA,
∴2∠BAM=90°-∠HBA,
∴∠BAM=45°-$\frac{1}{2}$∠HBA.
点评 本题为四边形的综合应用,涉及知识点有矩形的性质、全等三角形和相似三角形的判定和性质、直角三角形的性质及勾股定理等.在(1)中求得AF=AB是解题的关键,在(2)中注意面积的和差关系,在(3)中证得∠BAG=2∠BAM是解题的关键.本题考查知识点较多,综合性很强,难度很大.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 摸球的次数m | 100 | 150 | 200 | 500 | 800 | 1000 |
| 摸到白球的次数n | 58 | 96 | 116 | 295 | 484 | 601 |
| 摸到白球的概率$\frac{m}{n}$ | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
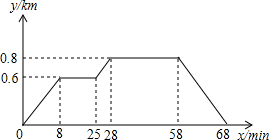 已知小明家、食堂、图书馆在同一直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系,根据图象可得,当25≤x≤28时,y与x的函数关系式是y=$\frac{1}{15}$x-$\frac{16}{15}$.
已知小明家、食堂、图书馆在同一直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.如图反映了这个过程中,小明离家的距离y与时间x之间的对应关系,根据图象可得,当25≤x≤28时,y与x的函数关系式是y=$\frac{1}{15}$x-$\frac{16}{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 居民户数 | 1 | 2 | 3 | 4 |
| 月用气量(立方米) | 14 | 15 | 22 | 25 |
| A. | 14 | B. | 15 | C. | 22 | D. | 25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com