
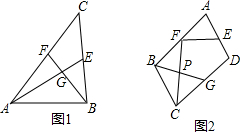
分析 解:(1)①解直角三角形得到BG=$\frac{1}{2}$AB=2,AG=ABcos60°=2$\sqrt{3}$,根据三角形的中位线的性质得到FG=$\frac{1}{2}$BG=1a2+b2=5c2,根据勾股定理即可得到结论;②同理得到AC=b=$\sqrt{21}$,BC=a=$\sqrt{39}$;
(2)根据(1)中的数据即可得到结论;
(3)取BC的中点H,连接HG,DB,如图2,根据三角形的中位线的性质得到EF∥DB∥HG,推出△BFP≌△PCG,根据全等三角形的性质得到P是BG的中点,然后根据(2)中的结论即可得到结果.
解答 解:(1)①∵AE⊥BF,∠ABF=60°,AB=4,
∴在Rt△ABG中,BG=$\frac{1}{2}$AB=2,AG=ABcos60°=2$\sqrt{3}$,
∵AE,BF是△ABC的中线,
∴FG=$\frac{1}{2}$BG=1a2+b2=5c2
在Rt△AGF中,AF=$\sqrt{A{G}^{2}+G{F}^{2}}$=$\sqrt{13}$,
∴AC=b=2$\sqrt{13}$,
同理可得BC=a=2$\sqrt{7}$;
②当∠ABF=30°,AB=2$\sqrt{3}$,
∴在Rt△ABG中,AG=$\frac{1}{2}$AB=$\sqrt{3}$,BG=AB•cos30°=3,
∴FG=$\frac{1}{2}$BG=$\frac{3}{2}$,
在Rt△AGF中,AF=$\sqrt{A{G}^{2}+G{F}^{2}}$=$\frac{\sqrt{21}}{2}$,
∴AC=b=$\sqrt{21}$,
同理得BC=a=$\sqrt{39}$,
故答案为:$\sqrt{39}$,$\sqrt{21}$;
(2)猜想:a2+b2=5c2,
由①可知,a2=28,b2=52,c2=16,
∵a2+b2=52+28=80=5×16=5c2,
∴a2+b2=5c2,
由②可知,a2=39,b2=21,c2=12,
∵a2+b2=39+21=60=5×12=5c2,
∴a2+b2=5c2,
故答案为a2+b2=5c2;
(3)取BC的中点H,连接HG,DB,如图2,
∵E,F,G分别是AD,AB,CD的中点,
∴EF∥DB∥HG,
∵BF∥CG,BF=CG,
∴∠BFP=∠GCP,
在△BFP与△PCG中,$\left\{\begin{array}{l}{∠BFP=∠GCP}\\{∠BPF=∠CPG}\\{BF=CG}\end{array}\right.$,
∴△BFP≌△PCG,
∴PF=CP,
∴P是BG的中点,
又∵EF⊥FC,
∴HG⊥PC,
由(2)可知BC2+BG2=5CG2,
∵AB=4$\sqrt{2}$,BC=3$\sqrt{2}$,
∴(3$\sqrt{2}$)2+BG2=5(2$\sqrt{2}$)2,
∴BG=$\sqrt{22}$.
点评 本题考查了平行四边形的性质,全等三角形的判定和性质,勾股定理,三角形的中位线的性质,正确的识别图形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
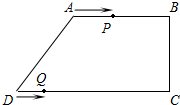 如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm.点P从点A出发,以3cm/s的速度沿折线ABCD方向运动,点Q从点D出发,以2cm/s的速度沿线段DC向点C运动.已知P,Q两点同时出发,当点Q到达点C时,P,Q停止运动,设运动时间为t(s).
如图,在四边形ABCD中,AB∥CD,∠BCD=90°,AB=AD=10cm,BC=8cm.点P从点A出发,以3cm/s的速度沿折线ABCD方向运动,点Q从点D出发,以2cm/s的速度沿线段DC向点C运动.已知P,Q两点同时出发,当点Q到达点C时,P,Q停止运动,设运动时间为t(s).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
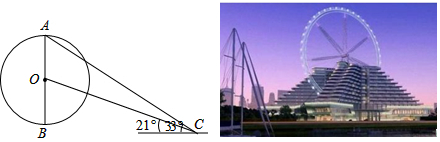
 如图所示,小明在绣湖公园的A处正面观测解百购物中心墙面上的电子屏幕,测得屏幕上端C处的仰角为30°,接着他正对电子屏幕方向前进7m到达B处,又测得该屏幕上端C处的仰角为45°.已知电子屏幕的下端离开地面距离DE为4m,小杨的眼睛离地面1.60m,电子屏幕的上端与墙体的顶端平齐.求电子屏幕上端与下端之间的距离CD(结果保留根号).
如图所示,小明在绣湖公园的A处正面观测解百购物中心墙面上的电子屏幕,测得屏幕上端C处的仰角为30°,接着他正对电子屏幕方向前进7m到达B处,又测得该屏幕上端C处的仰角为45°.已知电子屏幕的下端离开地面距离DE为4m,小杨的眼睛离地面1.60m,电子屏幕的上端与墙体的顶端平齐.求电子屏幕上端与下端之间的距离CD(结果保留根号).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 实数a,n,m,b满足a<n<m<b,这四个数在数轴上对应的点分别为A,N,M,B(如图),若AM2=BM•AB,BN2=AN•AB,则称m为a,b的“大黄金数”,n为a,b的“小黄金数”,当b-a=2时,a,b的大黄金数与小黄金数之差m-n=2$\sqrt{5}$-4.
实数a,n,m,b满足a<n<m<b,这四个数在数轴上对应的点分别为A,N,M,B(如图),若AM2=BM•AB,BN2=AN•AB,则称m为a,b的“大黄金数”,n为a,b的“小黄金数”,当b-a=2时,a,b的大黄金数与小黄金数之差m-n=2$\sqrt{5}$-4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 169米 | B. | 204米 | C. | 240米 | D. | 407米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com