Question

13．在三角形ABC中，∠C=θ，∠B=2θ，其中0°＜θ＜60°，圆心是A及半径是AB的圆与AC相交于D，并与BC相交（若需要可延长BC）相交于B、E（E可与B重合），那么EC=AD成立的条件是（　　）

• A． 没有θ的值可适合
• B． 仅当θ=45°
• C． 仅当0°＜θ≤45°
• D． 仅当45°≤θ＜60°
• E． 对于所有满足0°＜θ＜60°的θ都适合

Answer 1

分析 分三种情况进行讨论：①当0°＜θ＜45°时，如图1，这时发现△AEC是等腰三角形，则AE=EC，而AE和AD是同圆的半径，所以相等，结论成立；
②当θ=45°时，如图2，这时点E与点B重合，△ABC是等腰直角三角形，与同圆的半径相等，结论仍然成立；
③当45°＜θ＜60°时，如图3，⊙A与CB的延长线交于点E，根据三角形的内角和计算∠CAE的度数，发现与∠C相等，所以△ACE也是等腰三角形，同理结论也成立．
所以EC=AD成立的条件是，对于所有满足0°＜θ＜60°的θ都适合．

解答 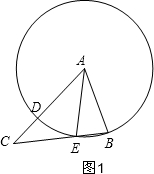解：①当0°＜θ＜45°时，如图1，
∵AB=AE，
∴∠AEB=∠ABC=2θ，
∵∠AEB=∠C+∠CAE，∠C=θ，
∴2θ=θ+∠CAE，
∴∠CAE=θ，
∴∠C=∠CAE，
∴AE=CE，
∵AE=AD，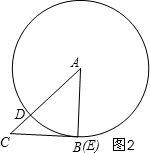
∴EC=AD；
所以当0°＜θ＜45°时，EC=AD成立；
②当θ=45°时，如图2，这时点E与点B重合，
∴∠C=45°，∠ABC=2θ=90°，
∴△ABC是等腰直角三角形，
∴AB=BC，
∵AB=AD，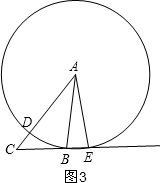
∴BC=AD，
即EC=AD，
所以θ=45°时，EC=AD成立；
③当45°＜θ＜60°时，如图3，⊙A与CB的延长线交于点E，
∵AB=AE，
∴∠ABE=∠AEB，
∵∠ABC=2θ，
∴∠ABE=∠AEB=180°-2θ，
∴∠BAE=180°-2（180°-2θ）=4θ-180°，
∵∠C=θ，∠ABC=2θ，
∴∠BAC=180°-3θ，
∴∠EAC=∠BAC+∠BAE=4θ-180°+180°-3θ=θ，
∴∠C=∠EAC，
∴AE=EC，
∵AE=AD，
∴EC=AD，
∴当45°＜θ＜60°时，EC=AD成立；
综上所述：EC=AD成立的条件是，对于所有满足0°＜θ＜60°的θ都适合．
故选E．

点评 本题是直线和圆的位置关系，考查了分类讨论的思想，本题是把三角形分为锐角三角形、直角三角形、钝角三角形三种情况讨论，利用了等腰三角形的性质：等边对等角，及同圆的半径相等、三角形的内角和定理，得出角相等，则边相等的关系．