
���� ���ݡ�������5ͷţ��2ֻ��ֵ��10����2ͷţ��5ֻ��ֵ��8�������õ�������ϵ�������г������飮
��� �⣺��ÿͷţֵ��x����ÿֻ��ֵ��y�������з�����Ϊ
$\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$��
�ʴ�Ϊ��$\left\{\begin{array}{l}{5x+2y=10}\\{2x+5y=8}\end{array}\right.$��
���� ���⿼������ʵ������������Ԫһ�η����飬�������Ĺؼ����ҵ���Ŀ�������ڵĵ�����ϵ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
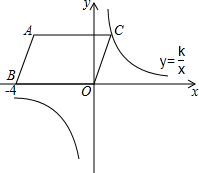 ��ͼ����ƽ��ֱ������ϵ�У��ı���ABOCΪƽ���ı��Σ�A��B������ֱ�Ϊ��-3��3������-4��0��������һ˫����y=$\frac{k}{x}$��ͼ����C��������˫���ߵı���ʽΪy=$\frac{3}{x}$��
��ͼ����ƽ��ֱ������ϵ�У��ı���ABOCΪƽ���ı��Σ�A��B������ֱ�Ϊ��-3��3������-4��0��������һ˫����y=$\frac{k}{x}$��ͼ����C��������˫���ߵı���ʽΪy=$\frac{3}{x}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ֱ��y=$\frac{1}{2}$x+1��y�ύ��A�㣬����A��������y=-$\frac{5}{4}$x2+bx+c��ֱ�߽�����һ��B������B��BC��x�ᣬ����Ϊ��C��3��0����
��ͼ��ֱ��y=$\frac{1}{2}$x+1��y�ύ��A�㣬����A��������y=-$\frac{5}{4}$x2+bx+c��ֱ�߽�����һ��B������B��BC��x�ᣬ����Ϊ��C��3��0�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
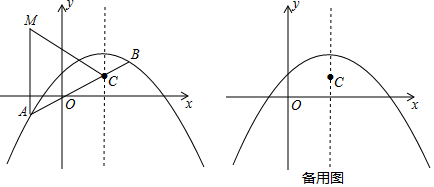
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com