
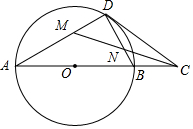
 如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连接BD,CM平分∠ACD,交BC于N,交AD于M
如图,在⊙O中,点C是直径AB延长线上一点,过点C作⊙O的切线,切点为D,连接BD,CM平分∠ACD,交BC于N,交AD于M分析 (1)欲证明DM=DN,只要证明∠DMN=∠DNM即可;
(2)连接OD交CM于E,作EF⊥AC于F.由△CDB∽△CAD,可得CD2=CB•CA=16,推出CD=4,由$\frac{{S}_{△CED}}{{S}_{△CEO}}$=$\frac{\frac{1}{2}•CD•DE}{\frac{1}{2}•OC•EF}$=$\frac{ED}{EO}$,可以推出$\frac{CD}{OC}$=$\frac{DE}{EO}$=$\frac{4}{5}$,推出DE=$\frac{4}{9}$OD=$\frac{4}{3}$,根据tan∠ACM=tan∠DCE=$\frac{ED}{CD}$=$\frac{\frac{4}{3}}{4}$=$\frac{1}{3}$,即可解决问题;
解答 (1)证明:连接OD.
∵CD是⊙O的切线,
∴CD⊥OD,
∴∠CDB+∠ODB=90°,
∵AB是直径,
∴∠ADB=90°,
∴∠A+∠ABD=90°,
∵OD=OB,
∴∠ABD=∠ODB,
∴∠CDB=∠A,
∵∠DNM=∠CDB+∠DCM,∠DMN=∠A+∠ACM,
∵∠DCM=∠ACM,
∴∠DNC=∠DMN,
∴DM=DN.
(2)连接OD交CM于E,作EF⊥AC于F.
由△CDB∽△CAD,可得CD2=CB•CA=16,
∴CD=4,
∵$\frac{{S}_{△CED}}{{S}_{△CEO}}$=$\frac{\frac{1}{2}•CD•DE}{\frac{1}{2}•OC•EF}$=$\frac{ED}{EO}$,
∵CM平分∠DCA,
∴ED=EF,
∴$\frac{CD}{OC}$=$\frac{DE}{EO}$=$\frac{4}{5}$,
∴DE=$\frac{4}{9}$OD=$\frac{4}{3}$,
∴tan∠ACM=tan∠DCE=$\frac{ED}{CD}$=$\frac{\frac{4}{3}}{4}$=$\frac{1}{3}$.
点评 本题考查切线的性质、解直角三角形、角平分线的性质定理、等腰三角形的判定、锐角三角函数等知识,解题关键是学会添加常用辅助线,灵活运用所学知识解决问题,学会用转化的思想思考问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
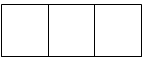 (1)如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母,每空中的字母不重复),请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率;
(1)如图,将A、B、C三个字母随机填写在三个空格中(每空填一个字母,每空中的字母不重复),请你用画树状图或列表的方法求从左往右字母顺序恰好是A、B、C的概率;查看答案和解析>>
科目:初中数学 来源: 题型:填空题
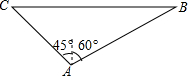 如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为(40+40$\sqrt{3}$)海里.
如图,一艘轮船在小岛A的北偏东60°方向且距小岛80海里的B处,沿正西方向航行一定时间后到达小岛的北偏西45°的C处,则该船航行的路程为(40+40$\sqrt{3}$)海里.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com