
【题目】已知直线AB∥CD.
(1)如图1,请直接写出∠BME、∠E、∠END的数量关系为 ;
(2)如图2,∠BME与∠CNE的角平分线所在的直线相交于点P,试探究∠P与∠E之间的数量关系,并证明你的结论;
(3)如图3,∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,直线MB、ND交于点F,则
∠NDE,直线MB、ND交于点F,则![]() =___.
=___.

【答案】(1)∠E=∠END-∠BME;(2)∠E+2∠NPM=180°,证明见解析;(3)![]() .
.
【解析】
(1)由AB∥CD,即可得到∠END=∠EFB,再根据∠EFB是△MEF的外角,即可得出∠E=∠EFB-∠BME=∠END-∠BME;
(2)由平行线的性质以及三角形外角性质,即可得到∠NPM=∠NGB+∠PMA=∠CNP+∠PMA,再根据三角形内角和定理,即可得到∠E+2∠PMA+2∠CNP=180°,即∠E+2(∠PMA+∠CNP)=180°,即可得到∠E+2∠NPM=180°;
(3)延长AB交DE于G,延长CD交BF于H,由平行线的性质以及三角形外角性质,即可得到∠E=∠ABE-∠AGE=∠ABE-∠CDE;依据∠CHB是△DFH的外角,即可得到∠F=∠CHB-∠FDH=![]() ∠ABE-
∠ABE-![]() ∠CDE=
∠CDE=![]() (∠ABE-∠CDE),进而得出∠F=
(∠ABE-∠CDE),进而得出∠F=![]() ∠E.
∠E.
解:(1)如图1,∵AB∥CD,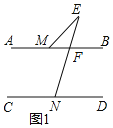
∴∠END=∠EFB,
∵∠EFB是△MEF的外角,
∴∠E=∠EFB-∠BME=∠END-∠BME,
故答案为:∠E=∠END-∠BME;
(2)如图2,∵AB∥CD,
∴∠CNP=∠NGB,
∵∠NPM是△GPM的外角,
∴∠NPM=∠NGB+∠PMA=∠CNP+∠PMA,
∵MQ平分∠BME,NP平分∠CNE,
∴∠CNE=2∠CNP,∠FME=2∠BMQ=2∠PMA,
∵AB∥CD,
∴∠MFE=∠CNE=2∠CNP,
∵△EFM中,∠E+∠FME+∠MFE=180°,
∴∠E+2∠PMA+2∠CNP=180°,
即∠E+2(∠PMA+∠CNP)=180°,
∴∠E+2∠NPM=180°;
(3)如图3,延长AB交DE于G,延长CD交BF于H,
∵AB∥CD,
∴∠CDG=∠AGE,
∵∠ABE是△BEG的外角,
∴∠E=∠ABE-∠AGE=∠ABE-∠CDE,①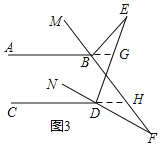
∵∠ABM=![]() ∠MBE,∠CDN=
∠MBE,∠CDN=![]() ∠NDE,
∠NDE,
∴∠ABM=![]() ∠ABE=∠CHB,∠CDN=
∠ABE=∠CHB,∠CDN=![]() ∠CDE=∠FDH,
∠CDE=∠FDH,
∵∠CHB是△DFH的外角,
∴∠F=∠CHB-∠FDH=![]() ∠ABE-
∠ABE-![]() ∠CDE=
∠CDE=![]() (∠ABE-∠CDE),②
(∠ABE-∠CDE),②
由①代入②,可得∠F=![]() ∠E,
∠E,
即![]() =
=![]() .
.
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】小颖为妈妈准备了一份生日礼物,礼物外包装盒为长方体形状,长、宽、高分别为![]() 、
、![]() 、
、![]()
![]() ,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为
,为了美观,小颖决定在包装盒外用丝带打包装饰,她发现,可以用如图所示的三种打包方式,所需丝带的长度分别为![]() ,
,![]() ,
,![]() (不计打结处丝带长度)
(不计打结处丝带长度)

(1)用含![]() 、
、![]() 、
、![]() 的代数式分别表示
的代数式分别表示![]() ,
,![]() ,
,![]() ;
;
(2)方法简介:
要比较两数![]() 与
与![]() 大小,我们可以将
大小,我们可以将![]() 与
与![]() 作差,结果可能出现三种情况:
作差,结果可能出现三种情况:
①![]() ,则
,则![]() ;
;
②![]() ,则
,则![]() ;
;
③![]() ,则
,则![]() ;
;
我们将这种比较大小的方法叫做“作差法”.
请帮小颖选出最节省丝带的打包方式,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初中生在数学运算中使用计算器的现象越来越普遍,某校一兴趣小组随机抽查了本校若干名学生使用计算器的情况.以下是根据抽查结果绘制出的不完整的条形统计图和扇形统计图: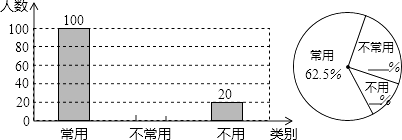
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是;
(2)请补全上述条形统计图和扇形统计图;
(3)若从这次接受调查的学生中,随机抽查一名学生恰好是“不常用”计算器的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,点D在AB边上,点D到点A的距离与点D到点C的距离相等.
(1)利用尺规作图作出点D,不写作法但保留作图痕迹.
(2)若△ABC的底边长5,周长为21,求△BCD的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,成都市青羊区有一块长为![]() 米,宽为
米,宽为![]() 米的长方形地块,角上有四个边长均为
米的长方形地块,角上有四个边长均为![]() 米的小正方形空地,开发商计划将阴影部分进行绿化.
米的小正方形空地,开发商计划将阴影部分进行绿化.
(1)用含![]() ,
,![]() 的代数式表示绿化的面积是多少平方米?(结果写成最简形式)
的代数式表示绿化的面积是多少平方米?(结果写成最简形式)
(2)若![]() ,
,![]() ,求出绿化面积.
,求出绿化面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知I是△ABC的内心,AI延长线交△ABC外接圆于D,连BD.
(1)在图1中,求证:DB=DI;
(2)如图2,若AB为直径,且OI⊥AD于I点,DE切圆于D点,求sin∠ADE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:对任意一个三位数![]() 如果
如果![]() 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与![]() 的商记为
的商记为![]() .例如
.例如![]() 对调百位与十位上的数字得到
对调百位与十位上的数字得到![]() 对调百位与个位上的数字得到
对调百位与个位上的数字得到![]() 对调十位与个位上的数字得到
对调十位与个位上的数字得到![]() 这三个新三位数的和为
这三个新三位数的和为![]() 所以
所以![]() .试根据以上信息,完成下列问题:
.试根据以上信息,完成下列问题:
(1)计算:![]() __,
__,![]() __,你从中发现什么规律?你发现规律是:__.
__,你从中发现什么规律?你发现规律是:__.
(2)若![]() 都是“相异数”,
都是“相异数”,![]()
![]() ,其中x是正整数),是否存在
,其中x是正整数),是否存在![]() 满足
满足![]() ,若存在,请求出这个
,若存在,请求出这个![]() ,若不存在,请说明理由.
,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为评估九年级学生的学习成绩状况,以应对即将到来的中考做好教学调整,某中学抽取了部分参加考试的学生的成绩作为样本分析,绘制成了如下两幅不完整的统计图,请根据图中提供的信息解答下列问题:
(1)求本中学成绩类别为“中”的人数;
(2)求出扇形图中,“优”所占的百分比,并将条形统计图补充完整;
(3)该校九年级共有1000人参加了这次考试,请估算该校九年级共有多少名学生的数学成绩达到优秀?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com