
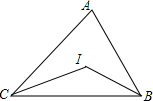
 如图,在△ABC中,∠ABC、∠ACB的平分线相交于点I,根据下列条件,求∠BIC的度数.
如图,在△ABC中,∠ABC、∠ACB的平分线相交于点I,根据下列条件,求∠BIC的度数.分析 (1)已知∠ABC=60°,∠ACB=70°,则角平分线所成的角度数为其度数的一半.然后根据三角形的内角和为180度求出∠CIB的度数.
(2)已知∠ABC+∠ACB=110°,∠ICB=$\frac{1}{2}$∠ACB,∠IBC=$\frac{1}{2}$∠ABC,∠ICB+∠IBC=$\frac{1}{2}$(∠ABC+∠ACB),然后根据三角形内角和为180度,求出∠CIB的度数.
(3)由于∠A=40°,则根据三角形内角和为180°得∠ABC+∠ACB的度数,然后根据分析(2)的方法求出∠CIB的度数.
(4)由于∠A=α,则根据三角形内角和为180°得∠ABC+∠ACB的度数,然后根据分析(2)的方法求出∠CIB的度数.
解答 解:(1)∠ICB=$\frac{1}{2}$∠ABC=30°,∠ICB=$\frac{1}{2}$∠ACB=35°,∠CIB=180°-30°-35°=115°;
(2)∠ICB+∠IBC=$\frac{1}{2}$(∠ABC+∠ACB)=55°,∠CIB=180°-55°=125°;
(3)∠ABC+∠ACB=180°-∠A=140°,∠ICB+∠IBC=$\frac{1}{2}$(∠ABC+∠ACB)=70°,∠CIB=180°-70°=110°;
(4)∠ABC+∠ACB=180°-∠A=180°-α,∠ICB+∠IBC=$\frac{1}{2}$(∠ABC+∠ACB)=90°-$\frac{1}{2}α$,∠CIB=180°-90°+$\frac{1}{2}α$=90°+$\frac{1}{2}α$;
故答案为:115°;125°;110°;90°+$\frac{1}{2}α$.
点评 本题考查三角形内角和问题,解题关键是得到∠ICB与∠IBC的和,在求解过程中主要用到定理:三角形的内角和为180°.


科目:初中数学 来源: 题型:解答题
 如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.
如图,矩形OABC的顶点A,C分别在x轴和y轴上,点B的坐标为(4,6).双曲线y=$\frac{k}{x}$(x>0)的图象经过BC的中点D,且与AB交于点E,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 1号 | 2号 | 3号 | 4号 | 5号 | 总数 | |
| 甲班 | 89 | 100 | 96 | 118 | 97 | 500 |
| 乙班 | 100 | 95 | 110 | 91 | 104 | 500 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com