
【题目】如图,AB为⊙O的直径,点C、D都在⊙O上,且CD平分∠ACB,交AB于点E.
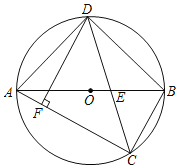
(1)求证:∠ABD=∠BCD;
(2)若DE=13,AE=17,求⊙O的半径;
(3)DF⊥AC于点F,试探究线段AF、DF、BC之间的数量关系,并说明理由.
【答案】(1)见解析;(2)12;(3)AF+BC=DF,理由见解析
【解析】
(1)由CD平分∠ACB,根据圆周角定理,可得∠ACD=∠BCD=∠ABD;
(2)过点E作EM⊥AD于点M,求出AD长,则AB=![]() AD,可求出AB,则答案得出;
AD,可求出AB,则答案得出;
(3)过点D作DN⊥CB,交CB的延长线于点N,可证明△DAF≌△DBN,则AF=BN,DF=CF则结论AF+BC=DF可得出.
(1)证明:∵CD平分∠ACB,
∴∠ACD=∠BCD,
∵∠ACD=∠ABD,
∴∠ABD=∠BCD;
(2)解:如图1,过点E作EM⊥AD于点M,

∵AB为⊙O的直径,
∴∠ACB=90°,∠ADB=90°,
∴∠DAB=∠BCD=45°,
∵AE=17,
∴ME=AM=17×![]() =
=![]() ,
,
∵DE=13,
∴DM=![]()
∴AD=AM+DM=![]() ,
,
∴AB=![]() AD=
AD=![]()
∴AO=![]() =12;
=12;
(3)AF+BC=DF.理由如下:
如图2,过点D作DN⊥CB,交CB的延长线于点N,

∵四边形DACB内接于圆,
∴∠DBN=∠DAF,
∵DF⊥AC,DN⊥CB,CD平分∠ACB,
∴∠AFD=∠DNB=90°,DF=DN,
∴△DAF≌△DBN(AAS),
∴AF=BN,CF=CN,
∵∠FCD=45°,
∴DF=CF,
∴CN=BN+BC=AF+BC=DF.
即AF+BC=DF.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C是⊙O上一点,![]() ,点D是AB上一点(点D与A,B不重合),连接CD.
,点D是AB上一点(点D与A,B不重合),连接CD.
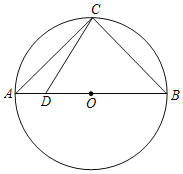
(1)用尺规作图,线段CD绕点C按逆时针方向旋转90°得到线段CE,连接DE交BC于点F,连接BE;(保留作图痕迹,不写作法.)
(2)当AD=BF时,求∠BEF的度数.
(3)求证:AD2+BD2=2CD2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于A(﹣2,0),点B(4,0).

(1)求抛物线的解析式;
(2)若点M是抛物线上的一动点,且在直线BC的上方,当S△MBC取得最大值时,求点M的坐标;
(3)在直线的上方,抛物线是否存在点M,使四边形ABMC的面积为15?若存在,求出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 方向向
方向向![]() 点运动,动点
点运动,动点![]() 从
从![]() 点出发,以每秒
点出发,以每秒![]() 个单位长度的速度沿着
个单位长度的速度沿着![]() 方向向
方向向![]() 点运动,如果
点运动,如果![]() ,
,![]() 两点同时出发,当
两点同时出发,当![]() 到达
到达![]() 点处时,两点都停止运动.设运动的时间为
点处时,两点都停止运动.设运动的时间为![]() 秒,
秒,![]() 的面积为
的面积为![]() .
.
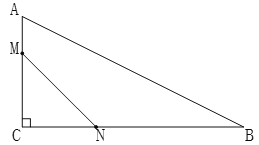
(1)用含![]() 的代数式表示:
的代数式表示:
![]() ,
,![]() ,
,![]() ;
;
(2)求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在硬地上抛掷一枚图钉,通常会出现两种情况:

下面是小明和同学做“抛掷图钉实验”获得的数据:
抛掷次数n | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
针尖不着地的频数m | 63 | 120 | 186 | 252 | 310 | 360 | 434 | 488 | 549 | 610 |
针尖不着地的频率 | 0.63 | 0.60 | 0.63 | 0.60 | 0.62 | 0.61 |
(1)填写表中的空格;
(2)画出该实验中,抛掷图钉钉尖不着地频率的折线统计图;

(3)根据“抛掷图钉实验”的结果,估计“钉尖着地”的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
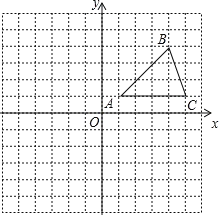
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形)。
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2、C2的坐标;
(3)在第(2)问中,点B旋转到点B2的过程中运动的路径长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在慈善一日捐活动中,学校团总支为了了解本校学生的捐款情况,随机抽取了50名学生的捐款数进行了统计,并绘制成下面的统计图.
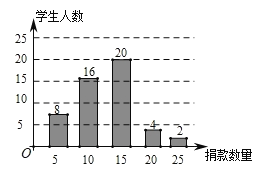
(1)这50名同学捐款的众数为 元,中位数为 元;
(2)该校共有600名学生参与捐款,请估计该校学生的捐款总数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】临近期末考试,心理专家建议考生可通过以下四种方式进行考前减压:![]() .享受美食,
.享受美食,![]() .交流谈心,
.交流谈心,![]() .体育锻炼,
.体育锻炼,![]() .欣赏艺术.
.欣赏艺术.
(1)随机采访一名九年级考生,选择其中某一种方式,他选择“享受美食”的概率是 .
(2)同时采访两名九年级考生,请用画树状图或列表的方法求他们中至少有一人选择“欣赏艺术”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com