
【题目】如图,在△ABC和△ADC中,已知AB=8,∠ACB=105°,∠B=45°,且∠ACB=∠BAD,∠B=∠D,则线段CD的长是____.

【答案】8
【解析】
作CE⊥AB于点E,作AF⊥CD于点F,根据已知可以求出∠CAE=30°,从而得到∠DAC =75°,∠DCA=60°,设 BE=CE=a,在RT△CAE中求出BE的值,,由于CF=CE=BE,从而得到AF及DF,从而得到CD的长度.
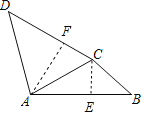
解:作CE⊥AB于点E,作AF⊥CD于点F,
则∠CED=∠CEB=90°,∠AFD=∠AFC=90°,
∵在△ABC中,∠ACB=105°,∠B=45°,∴∠CAE=30°,∴∠ECA=60°,
∵∠ACB=105°,∠B=45°,且∠ACB=∠BAD,∠B=∠D,
∴∠D=45°,∠BAD=105°,
∴∠DAC=∠BAD-∠CAE=75°,
∴∠DCA=60°,∠CAF=30°
设BE=a,则CE=a,AE=8-a,
∵∠CAE=30°,∠CEA=90°,
∴![]() =tan30°,
=tan30°,
解得,a=4(![]() -1),
-1),
∴AC=2a=8(![]() -1),
-1),
∵∠AFC=90°,∠ACF=60°,
∴CF=4(![]() -1),AF=12-4
-1),AF=12-4![]() ,
,
∵∠AFD=90°,∠D=45°,
∴DF=AF=12-4![]() ,
,
∴CD=DF+CF=12-4![]() +4(
+4(![]() -1)=8,
-1)=8,
故答案为:8.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】如图,∠BAC=90°,BD⊥DE,CE⊥DE,添加下列条件后仍不能使△ABD≌△CAE的条件是( )
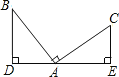
A. AD=AE B. AB=AC C. BD=AE D. AD=CE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 我们定义:如图1、图2、图3,在△ABC中,把AB绕点A顺时针旋转α(0°<α<180°)得到AB′,把AC绕点A逆时针旋转β得到AC′,连接B′C′,当α+β=180°时,我们称△AB'C′是△ABC的“旋补三角形”,△AB′C′边B'C′上的中线AD叫做△ABC的“旋补中线”,点A叫做“旋补中心”.图1、图2、图3中的△AB′C′均是△ABC的“旋补三角形”.
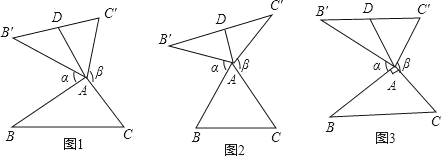
(1)①如图2,当△ABC为等边三角形时,“旋补中线”AD与BC的数量关系为:AD= BC;
②如图3,当∠BAC=90°,BC=8时,则“旋补中线”AD长为 .
(2)在图1中,当△ABC为任意三角形时,猜想“旋补中线”AD与BC的数量关系,并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某年级共有330名男生,为了解该年级男生1000米跑步成绩(单位:分/秒)的情况,从中随机抽取30名男生进行测试,获得了他们的相关成绩,并对数据进行整理、描述和分析.下面给出了部分信息.
a.1000米跑步的频数分布表如下:
分组 | 3′17″<x≤3′ 37″ | 3′37″<x≤3′ 57″ | 3′ 57″<x≤4′ 17″ | 4′ 17″<x≤4′ 37″ | 4′ 37″<x≤4′ 57″ | 4′ 57″<x≤5′ 17″ |
频数 | 10 | 9 | m | 2 | 2 | 1 |
注:3′37″即3分37秒
b.1000米跑步在3′37″<x≤3′57″这一组是:
3′39 ″ 3′42 ″ 3′45 ″ 3′45″ 3′50 ″ 3′52 ″ 3′53″ 3′55″ 3′57″
根据以上信息,回答下列问题:
(1)表中m的值为 ;
(2)根据表频数分布表画出相应的频数分布直方图.
(3)若男生1000米跑步成绩等于或者优于3′52″,成绩记为优秀.请估计全年级男生跑步成绩达到优秀的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
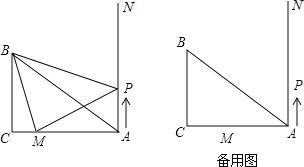
【题目】如图,在 Rt△ABC 中,∠C=90°,AC=8cm,BC=6cm,M 在 AC上,且AM=6cm,过点 A(与 BC 在 AC 同侧)作射线 AN⊥AC,若动点 P 从点 A 出发,沿射线 AN 匀速运动,运动速度为 1cm/s,设点 P 运动时间为 t 秒.
(1)经过 秒时,Rt△AMP 是等腰直角三角形?
(2)经过几秒时,PM⊥MB?
(3)经过几秒时,PM⊥AB?
(4)当△BMP 是等腰三角形时,直接写出 t 的所有值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①CF=2AF;②tan∠CAD=![]() ;
;
③DF=DC;④△AEF∽△CAB;⑤ S四边形CDEF=![]() S△ABF ,其中正确的结论有( )
S△ABF ,其中正确的结论有( )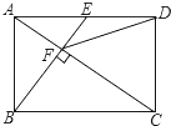
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了![]() 层,将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为
层,将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为![]()
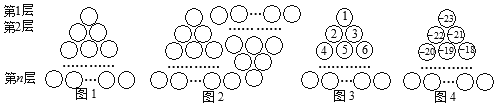
如果图中的圆圈共有13层,请解决下列问题:
(1)若自上往下,在图①每个圆圈中填上一串连续的正整数1,2,3,4,…,得到图3,写出第11层最左边这个圆圈中的数;
(2)若自上往下,在图①每个圆圈中填上一串连续的整数-23,-22,-21,20,…,得到图4,写出第10层最右边圆圈内的数;
(3)根据以上规律,求图4中第1层到第10层所有圆圈中各数之和(写出计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】陆老师布置了一道题目:过直线l外一点A作l的垂线.(用尺规作图)
小淇同学作法如下:
(1)在直线l上任意取一点C,连接AC;
(2)作AC的中点O;
(3)以O为圆心,OA长为半径画弧交直线l于点B,如图所示;
(4)作直线AB.
则直线AB就是所要作图形.
你认为小淇的作法正确吗?如果不正确,请画出一个反例;如果正确,请给出证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:![]()
![]()
![]()
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为![]() 和
和![]() (其中
(其中![]() 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
(3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com