
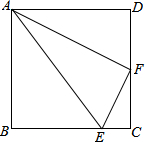
 设点E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,BE=3EC,F为CD的中点,连结AF,AE,EF.问△AEF是什么形状的三角形?请说明理由.
设点E,F分别是正方形ABCD中BC和CD边上的点,且AB=4,BE=3EC,F为CD的中点,连结AF,AE,EF.问△AEF是什么形状的三角形?请说明理由.科目:初中数学 来源: 题型:
 如图,抛物线y=ax2+bx+c(a≠0)经过点A(-6,0),B(2,0),C(0,-6)
如图,抛物线y=ax2+bx+c(a≠0)经过点A(-6,0),B(2,0),C(0,-6)查看答案和解析>>
科目:初中数学 来源: 题型:
| m2+1 |
| 2 |
| m2+2 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
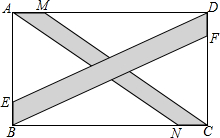 如图,在矩形ABCD中,点E、F在AB、CD上,BF∥DE,若AD=12,AB=7,且AE:EB=5:2,又有点M,N也在AD、BC上,且AM:MD=1:5,AN∥MC,求S空白.
如图,在矩形ABCD中,点E、F在AB、CD上,BF∥DE,若AD=12,AB=7,且AE:EB=5:2,又有点M,N也在AD、BC上,且AM:MD=1:5,AN∥MC,求S空白.查看答案和解析>>
科目:初中数学 来源: 题型:
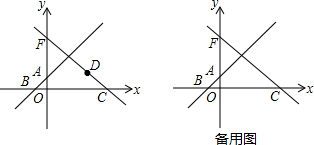 在平面直角坐标系xOy中,直线AB与直线y=-
在平面直角坐标系xOy中,直线AB与直线y=-| 3 |
| 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
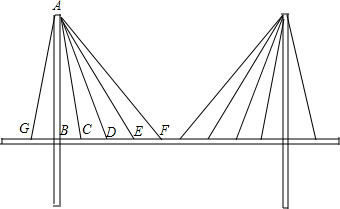 二次根式的加减在日常生活中有着广泛的应用.如在一座斜拉桥上可以看到很多拉索.如图所示,事实上,AB⊥GF.若AB=24m,BC=2m,BC=CD=DE=EF,桥的两个立柱两边各拉4条这样的拉索,那么拉索的总长度是多少米?
二次根式的加减在日常生活中有着广泛的应用.如在一座斜拉桥上可以看到很多拉索.如图所示,事实上,AB⊥GF.若AB=24m,BC=2m,BC=CD=DE=EF,桥的两个立柱两边各拉4条这样的拉索,那么拉索的总长度是多少米?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com