
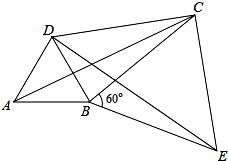
 给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.
给出定义,若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称该四边形为勾股四边形.分析 (1)首先证明△ABC≌△DBE,得出AC=DE,BC=BE,连接CE,进一步得出△BCE为等边三角形;
(2)利用等边三角形的性质,进一步得出△DCE是直角三角形,问题得解.
解答 解:(1)∵△ABC≌△DBE,
∴BC=BE,
∵∠CBE=60°,
∴△BCE是等边三角形;
(2)∵△ABC≌△DBE,
∴BE=BC,AC=ED;
∴△BCE为等边三角形,
∴BC=CE,∠BCE=60°,
∵∠DCB=30°,
∴∠DCE=90°,
在Rt△DCE中,
DC2+CE2=DE2,
∴DC2+BC2=AC2.
即四边形ABCD是勾股四边形.
点评 此题主要考查勾股定理,三角形的判定与性质,等边三角形的判定与性质,是一道综合性很强的题目.解决本题的关键是证明△BCE是等边三角形.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:选择题
 一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0:③b>0;④x<2时,kx+b<x+a中,正确的个数是( )
一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0:③b>0;④x<2时,kx+b<x+a中,正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 抛物线y=x2+bx+c经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.
抛物线y=x2+bx+c经过A(0,2),B(3,2)两点,若两动点D、E同时从原点O分别沿着x轴、y轴正方向运动,点E的速度是每秒1个单位长度,点D的速度是每秒2个单位长度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com