练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    　　如图，

     

     

     

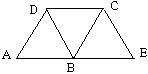
    （1）∵∠ABD=∠BDC（已知），∴　　　　 ∥　　　　 ，（　　　　　　  ）；

    　　    （2）∵∠DBC=∠ADB（已知），∴　　　　 ∥　　　　 ，（　　　　　　 ）；

    　　    （3）∵∠CBE=∠DCB（已知），∴　　　　 ∥　　　　 ，（　　　　　　 ）；

    　　    （4）∵∠CBE=∠A，（已知），∴　　　　  ∥　　　　 ，（　　　　　　 ）；

    　　    （5）∵∠A+∠ADC=180º（已知），∴　　    ∥　　    ，（　　　　　　 ）；

    　　    （6）∵∠A+∠ABC=180º（已知），∴　　    ∥　　    ，（　　　　　　   ）.

     

    答案：
    解析：

    		答案：（1）CD∥AB，内错角相等，两直线平行；（2）AD∥BC，内错角相等，两直线平行；

         （3）CD∥BE，内错角相等，两直线平行；（4）AD∥BC，同位角相等，两直线平行.

         （5）AB∥CD，同旁内角互补，两直线平行；（6）AD∥BC，同旁内角互补，两直线平行.

     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：数学教研室 题型：022

    　　根据题意填充理由：

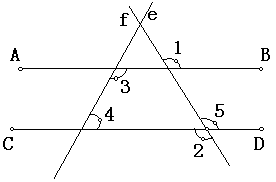
    已知：如左下图所示，∠1 = ∠2 .

    求证：∠3 + ∠4 = 180°.

    证明：∵ ∠5 = ∠2 .（　　　　　　　　　　　　　　　　    ）.

    　　  又 ∠1 = ∠2. （已知）.

    ∴  ∠5 = ∠1 （　　　　　　　　　　　　　　　　    ）.

    ∴ AB ∥ CD.(　　　　　　　　　　　　　　　　　　   ).

    ∴  ∠3 + ∠4 = 180°.(　　 　　　　　　　　　　　　　　　　　　　　  ).

     

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：044

    　　八年级某班进行小制作评比，作品上交时间为5月1日至30日，评委把同学上交作品的件数按5天一组分组统计绘制了频数直方图如图。已知从左到右各长方形的高的比为2:3:4:6:4:1，第三组的频数为12。

    （1）    本次活动共有多少件作品参评？

    （2）    哪组上交的作品数量最多？有多少件？

    （3）    经过评比，第四组与第六组分别有10件与2件获奖，那么这两组中哪组的获奖率较高？

    　　　　　　　　　　　　　　　　　　　　    频率

     

     

    　　　　　　　　　　　　　　　　　　   6

    　　　　　　　　　　　　　　　　  　　 5

    　　　　　　　　　　　　　　　　　　   4

    　　　　　　　　　　　　　　　　　　   3

    　　　　　　　　　　　　　　　　　　   2

    　　　　　　　　　　　　　　　　　　   1  　　　　　　　　　　   日期

    　　　　　　　　　　　　　　　　　　　　  

        　　　　　　　　　　　　　　　　　　　　1  6 11 16 21 26  31

     

    查看答案和解析>>

    科目：初中数学 来源：2014届安徽太和实验中学七年级下第一次月考数学试卷（解析版） 题型：解答题

    填空并完成推理过程．

    　　　（1）如图（1），，（已知）

    　　　　　　　　　　＝．(　　　　　　　　　　　　　　　)

    　　　　　　，(已知)

    　　　　　　＝　　　　　　，(　　　　　　　　　　　　　　)

    　　　　　　＝　　　　　　；(　　　　　　　　　　　　　　　)

    　　　（2）如图（2），已知，，．试判断与的关系，并说明你的理由．

    　 解：，理由是：，．(已知)

    　　　　　　　　　　　　＝　　　　　＝．(　　　　　　　　)

    　　　　　　　，(　　　　　　　　)

    　　　　　　　，即．

    　　　　　　　　　　　　　　　　　　；(　　　　　　　　　　　　　　　　

    (3) 如图(3)，点为上的点，点为上的点，，，试说明：．

    　　解：，(已知)，(　　　　　　　　　　　　　)

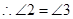    　　　　　　，(等量代换)

    　　　　　　　　　　　　，(　　　　　　　　　　　　　　　　　　　　)

    　　　　，(　　　　　　　　　　　　　　　　　　　　　)

    　　　　又，(已知)

    　　　　，(　　　　　　　　　　　　　)

    　　　　．(　　　　　　　　　　　　　　　　　　　　　　　　　　　)

    　

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如下图，E是ABCD的边AB上的一点，射线CE交BD于F，交DA的延长线于点G，AE：EB=1：2．图中有哪些位似三角形?位似中心分别是哪一个点?位似比分别为多少?填在下表中．

      位似三角形　　　

      位似中心　　　　　　　　

        位似比　　　　　　　　

    △GAE与△CBE　　

        点E　　　　　　　　

        1：2　　　　　　　　　

    　　　　　　　　　　　　

    　　　　　　　　　　　

    　　　　　　　　　　

    　　　　　　　　　　　　　　

    　　　　　　　　　　　　　

    　　　　　　　　　　

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    探索勾股定理时，我们发现“用不同的方式表示同一图形的面积”可以解决线段和（或差）的有关问题，这种方法称为面积法。请你运用面积法求解下列问题：在等腰三角形ABC中，AB=AC,BD为腰AC上的高。

    (1)若BD=h，M时直线BC上的任意一点，M到AB、AC的距离分别为。

    ①　　 若M在线段BC上，请你结合图形①证明：= h；　　　　　　　　　　

    ②　　 当点M在BC的延长线上时，，h之间的关系为　　　　　 （请直接写出结论，不必证明）　　　　　　　　　　　　　　　　　　　　　　　　　

    （2）如图②，在平面直角坐标系中有两条直线：y = x + 6 ； ：y = -3x+6 若上的一点M到的距离是3，请你利用以上结论求解点M的坐标。

    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

    　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 图②


    查看答案和解析>>

    同步练习册答案