
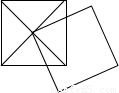
 如图所示,边长为a的两个正方形,其中一个正方形的一个顶点恰巧在另一个正方形的中心上,则它们重叠部分(阴影部分)的面积为 .
如图所示,边长为a的两个正方形,其中一个正方形的一个顶点恰巧在另一个正方形的中心上,则它们重叠部分(阴影部分)的面积为 . 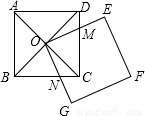
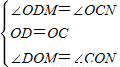 ,
, A2,
A2, a2,
a2, a2.
a2.

 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:初中数学 来源: 题型:
 将△OAB绕点O顺时针旋转30°后,得到△OB′A′,点A′恰好落在双曲线y=
将△OAB绕点O顺时针旋转30°后,得到△OB′A′,点A′恰好落在双曲线y=| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:
 23、高为50cm,底面周长为50cm的圆柱,在此圆柱的侧面上划分(如图所示)边长为lcm的正方形,用四个边长为lcm的小正方形构成“T”字形,用此图形是否能拼成圆柱侧面?试说明理由.
23、高为50cm,底面周长为50cm的圆柱,在此圆柱的侧面上划分(如图所示)边长为lcm的正方形,用四个边长为lcm的小正方形构成“T”字形,用此图形是否能拼成圆柱侧面?试说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,边长为1 的正方形网格中有格点△ABC(顶点是网格线的交点)和格点O,若把△ABC绕点O逆时针旋转90°.
如图所示,边长为1 的正方形网格中有格点△ABC(顶点是网格线的交点)和格点O,若把△ABC绕点O逆时针旋转90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com