
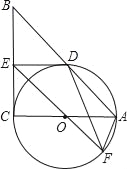
【题目】如图,在Rt△ABC中,∠C=90°,以AC为直径作⊙O,交AB于D,过点O作OE∥AB,交BC于E.
(1)求证:ED为⊙O的切线;
(2)若⊙O的半径为3,ED=4,EO的延长线交⊙O于F,连DF、AF,求△ADF的面积.
【答案】(1)见解析;(2)△ADF的面积是![]() .
.
【解析】试题分析:(1)连接OD,CD,求出∠BDC=90°,根据OE∥AB和OA=OC求出BE=CE,推出DE=CE,根据SSS证△ECO≌△EDO,推出∠EDO=∠ACB=90°即可;
(2)过O作OM⊥AB于M,过F作FN⊥AB于N,求出OM=FN,求出BC、AC、AB的值,根据sin∠BAC=![]() ,求出OM,根据cos∠BAC=
,求出OM,根据cos∠BAC=![]() ,求出AM,根据垂径定理求出AD,代入三角形的面积公式求出即可.
,求出AM,根据垂径定理求出AD,代入三角形的面积公式求出即可.
试题解析:
(1)证明:连接OD,CD,

∵AC是⊙O的直径,
∴∠CDA=90°=∠BDC,
∵OE∥AB,CO=AO,
∴BE=CE,
∴DE=CE,
∵在△ECO和△EDO中
 ,
,
∴△ECO≌△EDO,
∴∠EDO=∠ACB=90°,
即OD⊥DE,OD过圆心O,
∴ED为⊙O的切线.
(2)过O作OM⊥AB于M,过F作FN⊥AB于N,

则OM∥FN,∠OMN=90°,
∵OE∥AB,
∴四边形OMFN是矩形,
∴FN=OM,
∵DE=4,OC=3,由勾股定理得:OE=5,
∴AC=2OC=6,
∵OE∥AB,
∴△OEC∽△ABC,
∴![]() ,
,
∴![]() ,
,
∴AB=10,
在Rt△BCA中,由勾股定理得:BC=![]() =8,
=8,
sin∠BAC=![]() ,
,
即![]() ,
,
OM=![]() =FN,
=FN,
∵cos∠BAC=![]() ,
,
∴AM=![]()
由垂径定理得:AD=2AM=![]() ,
,
即△ADF的面积是![]() AD×FN=
AD×FN=![]() ×
×![]() ×
×![]() =
=![]() .
.
答:△ADF的面积是![]() .
.


科目:初中数学 来源: 题型:
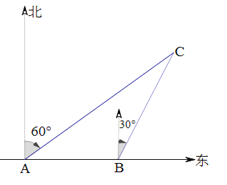
【题目】如图,一艘渔船以30海里/h的速度由西向东追赶鱼群.在A处测得小岛C在船的北偏东60°方向;40min后渔船行至B处,此时测得小岛C在船的北偏东![]() 方向.问:小岛C于渔船的航行方向的距离是________________海里(结果可用带根号的数表示).
方向.问:小岛C于渔船的航行方向的距离是________________海里(结果可用带根号的数表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
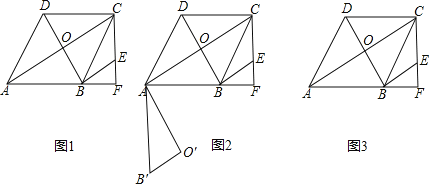
【题目】如图1,在菱形ABCD中,∠DAB=60°,AB=8![]() ,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
,对角线交于点O,CF垂直AB交AB的延长线于点F,过点B作BE∥AC交FC于EF.
(1)求BE的长:
(2)如图2,在OB上有一动点P,将△AOB绕A点顺时针旋转90°至△AOB',P点的对应点为P′,现有一动点Q从P点出发,沿着适当路径先运动到O′点,再沿O′A运动至A点,再从A点沿适当的路径运动至P′点.求Q点的最短运动路径的长;
(3)若△ABO以每秒2![]() 个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
个单位长度的速度沿射线AB向右平移,得到三角形△A1B1O1,当A1与点F重合时停止移动,设运动时间为t,在这个过程中,点O1关于直线BC的对称点为O″,当O″,F,C三点构成的三角形为等腰三角形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
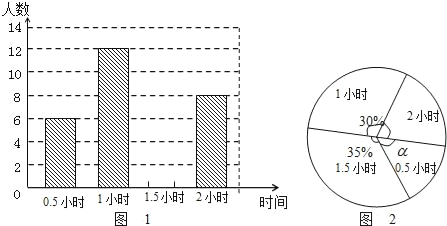
【题目】为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人;
(2)图2中α是 度,并将图1条形统计图补充完整;
(3)请估算该校九年级学生自主学习时间不少于1.5小时有 人;
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
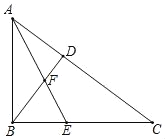
【题目】如图,在△ABC中,∠ABC=90°,BD⊥AC,垂足为D,E为BC边上一动点(不与B、C重合),AE、BD交于点F.
(1)当AE平分∠BAC时,求证:∠BEF=∠BFE;
(2)当E运动到BC中点时,若BE=2,BD=2.4,AC=5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)
问题提出:用n根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
问题探究:不妨假设能搭成![]() 种不同的等腰三角形,为探究
种不同的等腰三角形,为探究![]() 之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
之间的关系,我们可以从特殊入手,通过试验、观察、类比,最后归纳、猜测得出结论.
探究一:
用3根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
此时,显然能搭成一种等腰三角形。所以,当![]() 时,
时,![]()
用4根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
只可分成1根木棒、1根木棒和2根木棒这一种情况,不能搭成三角形
所以,当![]() 时,
时,![]()
用5根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和3根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和1根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
用6根相同的木棒搭成一个三角形,能搭成多少种不同的三角形?
若分成1根木棒、1根木棒和4根木棒,则不能搭成三角形
若分为2根木棒、2根木棒和2根木棒,则能搭成一种等腰三角形
所以,当![]() 时,
时,![]()
综上所述,可得表①
| 3 | 4 | 5 | 6 |
| 1 | 0 | 1 | 1 |
探究二:
用7根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(仿照上述探究方法,写出解答过程,并把结果填在表②中)
分别用8根、9根、10根相同的木棒搭成一个三角形,能搭成多少种不同的等腰三角形?
(只需把结果填在表②中)
| 7 | 8 | 9 | 10 |
|
你不妨分别用11根、12根、13根、14根相同的木棒继续进行探究,……
解决问题:用![]() 根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?
(设![]() 分别等于
分别等于![]() 、
、![]() 、
、![]() 、
、![]() ,其中
,其中![]() 是整数,把结果填在表③中)
是整数,把结果填在表③中)
|
|
|
|
|
|
问题应用:用2016根相同的木棒搭一个三角形(木棒无剩余),能搭成多少种不同的等腰三角形?(要求写出解答过程)
其中面积最大的等腰三角形每个腰用了__________________根木棒。(只填结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
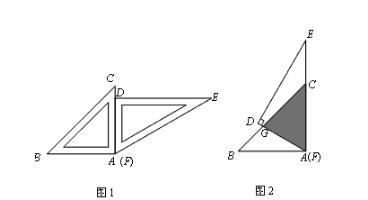
【题目】一副三角板按图1所示的位置摆放,将△DEF绕点A.F)逆时针旋转60°后(图2),测得CG=10cm,则两个三角形重叠(阴影)部分的面积为()
A. 75cm2; B. (25+25![]() )cm2; C. (25+
)cm2; C. (25+![]() )cm2; D. (25+
)cm2; D. (25+![]() )cm2
)cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠AOB是一钢架,∠AOB=15°,为使钢架更加牢固,需在其内部添加一些钢管EF、FG、GH…添的钢管长度都与OE相等,则最多能添加这样的钢管( )根.

A. 2 B. 4 C. 5 D. 无数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),已知小正方形![]() 的面积为1,把它的各边延长一倍得新正方形
的面积为1,把它的各边延长一倍得新正方形![]() ;把正方形
;把正方形![]() 边长按原法延长一倍得到正方形
边长按原法延长一倍得到正方形![]() 如图(2);以此下去,则正方形
如图(2);以此下去,则正方形![]() 的面积为_________________.
的面积为_________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com