
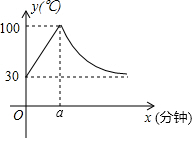
 教室内的饮水机接通电源进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(分钟)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为30℃时,接通电源后,水温y(℃)和时间x(分钟)的关系如图.
教室内的饮水机接通电源进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(分钟)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.如图为在水温为30℃时,接通电源后,水温y(℃)和时间x(分钟)的关系如图.分析 (1)根据题意和函数图象可以求得a的值;
(2)根据函数图象和题意可以求得y关于x的函数关系式,注意函数图象是循环出现的;
(3)根据(2)中的函数解析式可以解答本题;
(4)根据题意和(3)中的结果可以解答本题.
解答 解:(1)由题意可得,
a=(100-30)÷10=70÷10=7,
故答案为:7;
(2)当0≤x≤7时,设y关于x的函数关系式为:y=kx+b,
$\left\{\begin{array}{l}{b=30}\\{7k+b=100}\end{array}\right.$,
得$\left\{\begin{array}{l}{k=10}\\{b=30}\end{array}\right.$,
即当0≤x≤7时,y关于x的函数关系式为y=10x+30,
当x>30时,设y=$\frac{a}{x}$,
100=$\frac{a}{7}$,得a=700,
即当x>30时,y关于x的函数关系式为y=$\frac{700}{x}$,
当y=30时,x=$\frac{70}{3}$,
∴y与x的函数关系式为:y=$\left\{\begin{array}{l}{10x+30(0≤x≤7)}\\{\frac{700}{x}(7≤x≤\frac{70}{3})}\end{array}\right.$,
(3)将y=70代入y=10x+30,得x=4,
将y=70代入y=$\frac{700}{x}$,得x=10,
∵10-4=6,
∴饮水机有6分钟能使水温保持在70℃及以上;
(4)由题意可得,
6+(70-20)÷10=11(分钟),
∴40-11=29,
即8:29开机接通电源比较合适.
点评 本题考查反比例函数的应用、一次函数的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想和函数的思想解答.


科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x=1}\\{y=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=2}\\{y=\frac{4}{3}}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=4}\\{y=3}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=7}\\{y=3}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
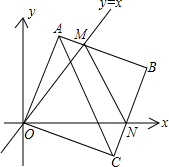 如图①,在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,O为坐标原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.
如图①,在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,O为坐标原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
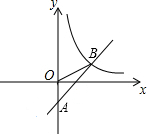 如图,在平面直角坐标系中,直线AB与y轴相交于点A(0,-2),与反比例函数在第一象限内的图象相交于点B(m,2),△AOB的面积为4.
如图,在平面直角坐标系中,直线AB与y轴相交于点A(0,-2),与反比例函数在第一象限内的图象相交于点B(m,2),△AOB的面积为4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com