
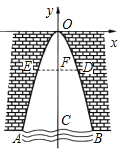
【题目】如图,一个涵洞的截面边缘是抛物线形.现测得当水面宽AB=1.6m时,涵洞顶点与水面的距离是2.4m.这时,离开水面1.5m处,涵洞的宽DE为_____.
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
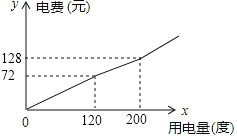
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湖南广益实验即将开展校园文化艺术节活动,为了合理编排节目,对学生最喜爱的歌曲、舞蹈、小品、相声四类节目进行了一次随机抽样调查(每名学生必须选择且只能选择一类),并将调查结果绘制成如下不完整统计图.
请你根据图中信息,回答下列问题:
(1)本次共调查了__________名学生;
(2)根据以上统计分析,估计该校2000名学生中最喜爱小品的人数为__________人;
(3)九年一班和九年二班各有2名学生擅长舞蹈,学校准备从这4名学生中随机抽取2名学生参加舞蹈节目的编排,那么抽取的2名学生恰好来自同一个班级的概率是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一不透明的布袋里,装有红、黄、蓝三种颜色的小球(除颜色外其余都相同),其中有红球2个,蓝球1个,黄球若干个,现从中任意摸出一个球是红球的概率为![]() .
.
(1)求口袋中黄球的个数;
(2)甲同学先随机摸出一个小球(不放回),再随机摸出一个小球,请用“树状图法”或“列表法”,
求两次摸 出都是红球的概率;
查看答案和解析>>
科目:初中数学 来源: 题型:
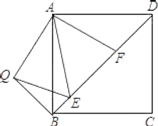
【题目】如图,在正方形ABCD中,E,F是对角线B上两点,且∠EAF=45°,将△ADF绕点A顺时针旋转90°后得到△ABQ,连接EQ,
求证:(1)EA是∠QAF的平分线;
(2)BD=BE+QE+QB.
查看答案和解析>>
科目:初中数学 来源: 题型:
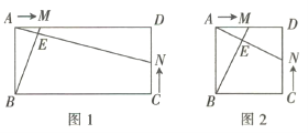
【题目】如图1,在矩形![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发向点
出发向点![]() 移动,速度为每秒1个单位长度,点
移动,速度为每秒1个单位长度,点![]() 从点
从点![]() 出发向点
出发向点![]() 移动,速度为每秒2个单位长度. 两点同时出发,且其中的任何一点到达终点后,另一点的移动同时停止.
移动,速度为每秒2个单位长度. 两点同时出发,且其中的任何一点到达终点后,另一点的移动同时停止.
(1)若两点的运动时间为![]() ,当
,当![]() 为何值时,
为何值时,![]() ?
?
(2)在(1)的情况下,猜想![]() 与
与![]() 的位置关系并证明你的结论.
的位置关系并证明你的结论.
(3)①如图2,当![]() 时,其他条件不变,若(2)中的结论仍成立,则
时,其他条件不变,若(2)中的结论仍成立,则![]() _________.
_________.
②当![]() ,
,![]() 时,其他条件不变,若(2)中的结论仍成立,则
时,其他条件不变,若(2)中的结论仍成立,则![]() _________(用含
_________(用含![]() 的代数式表示).
的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,OA=2,OB=4,以A点为顶点,AB为腰在第三象限作等腰直角△ABC.

(1)求C点的坐标.
(2)如图2,OA=2,P为y轴负半轴上的一个动点,若以P为直角顶点,PA为腰作等腰直角△APD,过D作DE⊥x轴于E点,求OP-DE的值.
(3)如图3,点F坐标为(-4,-4),点G(0,m)在y轴负半轴,点H(n,0)在x轴的正半轴,且FH⊥FG,求m+n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把二次涵数![]() 的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数
的图象先向左平移2个单位长度,再向上平移4个单位长度,得到二次函数![]() 的图象.
的图象.
(1)试确定![]() ,
,![]() ,
,![]() 的值;
的值;
(2)指出二次函数![]() 图象的开口方向、对称轴和顶点坐标.
图象的开口方向、对称轴和顶点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
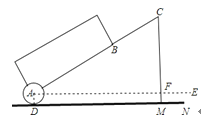
【题目】一种拉杆式旅行箱的示意图如图所示,箱体长AB=50cm,拉杆最大伸长距离BC=35cm,(点A、B、C在同一条直线上),在箱体的底端装有一圆形滚轮⊙A,⊙A与水平地面切于点D,AE∥DN,某一时刻,点B距离水平面38cm,点C距离水平面59cm.
(1)求圆形滚轮的半径AD的长;
(2)当人的手自然下垂拉旅行箱时,人感觉较为舒服,已知某人的手自然下垂在点C处且拉杆达到最大延伸距离时,点C距离水平地面73.5cm,求此时拉杆箱与水平面AE所成角∠CAE的大小(精确到1°,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com