
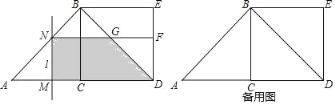
【题目】如图,△ABC中,∠ACB=90°,AC=CB=2,以BC为边向外作正方形BCDE,动点M从A点出发,以每秒1个单位的速度沿着A→C→D的路线向D点匀速运动(M不与A、D重合);过点M作直线l⊥AD,l与路线A→B→D相交于N,设运动时间为t秒:
(1)填空:当点M在AC上时,BN= (用含t的代数式表示);
(2)当点M在CD上时(含点C),是否存在点M,使△DEN为等腰三角形?若存在,直接写出t的值;若不存在,请说明理由;
(3)过点N作NF⊥ED,垂足为F,矩形MDFN与△ABD重叠部分的面积为S,求S的最大值.
【答案】(1)BN=2![]() ﹣
﹣![]() t;(2)当t=4﹣
t;(2)当t=4﹣![]() 或t=3或t=2时,△DNE是等腰三角形;(3)当t=
或t=3或t=2时,△DNE是等腰三角形;(3)当t=![]() 时,S取得最大值
时,S取得最大值![]() .
.
【解析】
(1)由等腰直角三角形的性质知AB=2![]() ,MN=AM=t,AN=
,MN=AM=t,AN=![]() ﹣AM=
﹣AM=![]() ﹣t,据此可得;
﹣t,据此可得;
(2)先得出MN=DM=4﹣t,BP=PN=t﹣2,PE=4﹣t,由勾股定理得出NE=![]() ,再分DN=DE,DN=NE,DE=NE三种情况分别求解可得;
,再分DN=DE,DN=NE,DE=NE三种情况分别求解可得;
(3)分0≤t<2和2≤t≤4两种情况,其中0≤t<2重合部分为直角梯形,2≤t≤4时重合部分为等腰直角三角形,根据面积公式得出面积的函数解析式,再利用二次函数的性质求解可得.
(1)如图1,
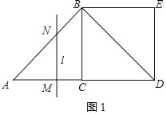
∵∠ACB=90°,AC=BC=2,
∴∠A=∠ABC=45°,AB=2![]() ,
,
∵AM=t,∠AMN=90°,
∴MN=AM=t,AN=![]() AM=
AM=![]() t,
t,
则BN=AB﹣AN=![]()
故答案为:![]()
(2)如图2,
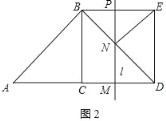
∵AM=t,AC=BC=CD=2,∠BDC=∠DBE=45°,
∴DM=MN=AD﹣AM=4﹣t,
∴DN=![]() DM=
DM=![]() (4﹣t),
(4﹣t),
∵PM=BC=2,
∴PN=2﹣(4﹣t)=t﹣2,
∴BP=t﹣2,
∴PE=BE﹣BP=2﹣(t﹣2)=4﹣t,
则NE=![]() ,
,
∵DE=2,
∴①若DN=DE,则![]() (4﹣t)=2,解得t=4﹣
(4﹣t)=2,解得t=4﹣![]() ;
;
②若DN=NE,则![]() (4﹣t)=
(4﹣t)=![]() ,解得t=3;
,解得t=3;
③若DE=NE,则2=![]() ,解得t=2或t=4(点N与点E重合,舍去);
,解得t=2或t=4(点N与点E重合,舍去);
综上,当t=4﹣![]() 或t=3或t=2时,△DNE是等腰三角形.
或t=3或t=2时,△DNE是等腰三角形.
(3)①当0≤t<2时,如图3,
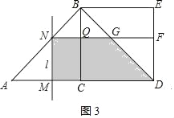
由题意知AM=MN=t,
则CM=NQ=AC﹣AM=2﹣t,
∴DM=CM+CD=4﹣t,
∵∠ABC=∠CBD=45°,∠NQB=∠GQB=90°,
∴NQ=BQ=QG=2﹣t,
则NG=4﹣2t,
∴![]()
当t=![]() 时,S取得最大值
时,S取得最大值![]() ;
;
②当2≤t≤4时,如图4,
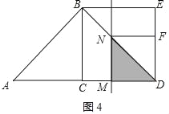
∵AM=t,AD=AC+CD=4,
∴DM=AD﹣AM=4﹣t,
∵∠DMN=90°,∠CDB=45°,
∴MN=DM=4﹣t,
∴S=![]() (4﹣t)2=
(4﹣t)2=![]() (t﹣4)2,
(t﹣4)2,
∵2≤t≤4,
∴当t=2时,S取得最大值2;
综上,当t=![]() 时,S取得最大值
时,S取得最大值![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两人相约元旦登山,甲、乙两人距地面的高度y(m)与登山时间x(min)之间的函数图像如图所示,根据图像所提供的信息解答下列问题:
(1)t= min.
(2)若乙提速后,乙登山的上升速度是甲登山的上升速度3倍,
①则甲登山的的上升速度是 m/min;
②请求出甲登山过程中,距地面的高度y(m)与登山时间x(min)之间的函数关系式.
③当甲、乙两人距地面高度差为70m时,求x的值(直接写出满足条件的x值).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+2的图象与y轴交于点A,与反比例函数y=![]() (k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=
(k≠0)在第一象限内的图象交于点B,且点B的横坐标为1.过点A作AC⊥y轴交反比例函数y=![]() (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
(1)求反比例函数的表达式.
(2)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关系哪些表示函数关系?
(1)在一定的时间t内,匀速运动所走的路程s和速度v;
(2)在平静的湖面上,投入一粒石子,泛起的波纹的周长L与半径r;
(3)正方形的面积S和梯形的面积S′;
(4)圆的面积S和它的周长C.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,在矩形ABCD中,对角线AC与BD相交于点O,过点O作直线EF⊥BD,且交AD于点E,交BC于点F,连接BE,DF,且BE平分∠ABD.
①求证:四边形BFDE是菱形;
②直接写出∠EBF的度数.
(2)把(1)中菱形BFDE进行分离研究,如图2,G,I分别在BF,BE边上,且BG=BI,连接GD,H为GD的中点,连接FH,并延长FH交ED于点J,连接IJ,IH,IF,IG.试探究线段IH与FH之间满足的关系,并说明理由;
(3)把(1)中矩形ABCD进行特殊化探究,如图3,矩形ABCD满足AB=AD时,点E是对角线AC上一点,连接DE,作EF⊥DE,垂足为点E,交AB于点F,连接DF,交AC于点G.请直接写出线段AG,GE,EC三者之间满足的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
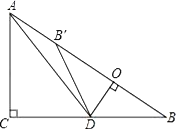
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D为边CB上的一个动点(点D不与点B重合),过D作DO⊥AB,垂足为O,点B′在边AB上,且与点B关于直线DO对称,连接DB′,AD.
(1)求证:△DOB∽△ACB;
(2)若AD平分∠CAB,求线段BD的长;
(3)当△AB′D为等腰三角形时,求线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,初中学生课桌椅不合格率达76.7%(不合格是指不能按照学生不同的身高来调节课桌椅的高度),为了解初中生的身高情况,随机抽取了某校初中部分男生、女生进行调查收集数据如下:
男生身高(单位:cm):163 161 160 163 161 162 163 164 163 163
女生身高(单位:cm):164 161 160 161 161 162 160 162 163 162
整理数据:
160 | 161 | 162 | 163 | 164 | |
男生(人) | 1 | 2 | 1 | a | 1 |
女生(人) | 2 | b | 3 | 1 | 1 |
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,并补全条形统计图;
(2)现有两名身高都为163cm的男生和女生,比较这两名同学分别在男生、女生中的身高情况,并简述理由;
(3)根据相关研究发现,只有身高为161cm的初中生课桌椅是合格的,试估计全校1000名学生中,有多少名学生的课桌椅是合格的?

查看答案和解析>>
科目:初中数学 来源: 题型:
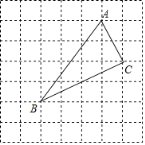
【题目】如图,在7×7网格中,每个小正方形的边长都为1.
(1)建立适当的平面直角坐标系后,若点A(1,3)、C(2,1),则点B的坐标为______;
(2)△ABC的面积为______;
(3)判断△ABC的形状,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com