
【题目】如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(4,0),另一个交点为A,且与y轴交于点C(0,4).
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,当 MN的值最大时,求△BMN的周长.
(3)在(2)的条件下,MN取得最大值时,若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,设平行四边形CBPQ的面积为S1,△ABN的面积为S2,且S1=4S2,求点P的坐标.

【答案】(1)抛物线的解析式为y=x2﹣5x+4;(2)4+4![]() ;(3)点P的坐标为P(3,﹣2).
;(3)点P的坐标为P(3,﹣2).
【解析】试题(1)利用待定系数法及直线BC上的两点列方程,从而得出一次函数的解析式;根据二次函数上面的两点坐标列出两个方程,从而确定二次函数的一次项系数和常数项;
(2)根据M,N的位置关系,易得他们的横坐标相同,设出对应的坐标,M(x,x2﹣5x+4)(1<x<4),则N(x,﹣x+4),根据两点坐标表示出MN的长度为MN=(﹣x+4)﹣(x2﹣5x+4)=﹣x2+4x,然后配方,求出MN的最大值;从而△BMN的周长得解;
(3)先求出△ABN的面积为S2,=3,再根据S1=4S2得S1=12.根据平行四边形的底边AB=![]() ,得出平行四边形的高线BD=
,得出平行四边形的高线BD=![]() ,再求x粥上面的BE的长度为3,得点E与点A重合,则过点A平行于BC的直线PQ为y=﹣x+1,最后与二次函数联立方程组,得出点P的坐标.
,再求x粥上面的BE的长度为3,得点E与点A重合,则过点A平行于BC的直线PQ为y=﹣x+1,最后与二次函数联立方程组,得出点P的坐标.
试题解析:
(1)设直线BC的解析式为y=mx+n,
将B(4,0),C(0,4)两点的坐标代入,
得,![]() ,
,
∴![]()
所以直线BC的解析式为y=﹣x+4;
将B(4,0),C(0,4)两点的坐标代入y=x2+bx+c,
得,![]() ,
,
∴![]()
所以抛物线的解析式为y=x2﹣5x+4;
(2)如图1,
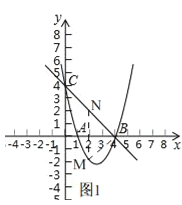
设M(x,x2﹣5x+4)(1<x<4),则N(x,﹣x+4),
∵MN=(﹣x+4)﹣(x2﹣5x+4)=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,MN有最大值4;
∵MN取得最大值时,x=2,
∴﹣x+4=﹣2+4=2,即N(2,2).
x2﹣5x+4=4﹣5×2+4=﹣2,即M(2,﹣2),
∵B(4.0)
可得BN=2![]() ,BM=2
,BM=2![]()
∴△BMN的周长=4+2![]() +2
+2![]() =4+4
=4+4![]()
(3)令y=0,解方程x2﹣5x+4=0,得x=1或4,
∴A(1,0),B(4,0),
∴AB=4﹣1=3,
∴△ABN的面积S2=×3×2=3,
∴平行四边形CBPQ的面积S1=4S2=12.
如图2,

设平行四边形CBPQ的边BC上的高为BD,则BC⊥BD.
∵BC=4![]() ,
,
∴BCBD=12,
∴BD=![]() .
.
过点D作直线BC的平行线,交抛物线与点P,交x轴于点E,在直线DE上截取PQ=BC,连接CQ,则四边形CBPQ为平行四边形.
∵BC⊥BD,∠OBC=45°,
∴∠EBD=45°,
∴△EBD为等腰直角三角形,由勾股定理可得BE=![]() BD=3,
BD=3,
∵B(4,0),
∴E(1,0),
设直线PQ的解析式为y=﹣x+t,
将E(1,0)代入,得﹣1+t=0,解得t=1
∴直线PQ的解析式为y=﹣x+1.
解方程组, ![]() ,
,
得,![]() 或
或![]() ,
,
∵P1(1,0)在x轴上,舍去.
∴点P的坐标为P(3,﹣2).


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() 分别平分
分别平分![]() 和
和![]() ,
,![]() 、
、![]() 交于点
交于点![]() .
.

(1)直接写出![]() 与
与![]() 的数量关系;
的数量关系;
(2)若![]() ,利用(1)的关系,求出
,利用(1)的关系,求出![]() 的度数;
的度数;
(3)利用(2)的结果,试判断![]() 、
、![]() 、
、![]() 的数量关系,并证明.
的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点O是等边![]() 内一点
内一点![]() 将
将![]() 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() 已知
已知![]()
![]() .
.
![]() 求证:
求证:![]() 是等边三角形;
是等边三角形;
![]() 当
当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
![]() 探究:当
探究:当![]() 为多少度时,
为多少度时,![]() 是等腰三角形.
是等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连接AD,将△ACD沿AD折叠,点C落在点C'处,连接C'D交AB于点E,连接BC',当△BC'D是直角三角形时,DE的长为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为学生装一台直饮水器,课间学生到直饮水器打水.他们先同时打开全部的水笼头放水,后来又关闭了部分水笼头.假设前后两人接水间隔时间忽略不计,且不发生泼洒,直饮水器的余水量![]() (升)与接水时间
(升)与接水时间![]() (分)的函数图象如图,请结合图象回答下列问题:
(分)的函数图象如图,请结合图象回答下列问题:

(1)求当![]() 时,
时,![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)假定每人水杯接水0.7升,要使40名学生接水完毕,课间10分钟是否够用?请计算回答.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
我区在一项工程招标时,接到甲、乙两个工程队的投标书,从投标书中得知:每施工一天,甲工程队要![]() 万元,乙工程队要
万元,乙工程队要![]() 万元,工程小组根据甲、乙两队标书的测算,有三种方案:
万元,工程小组根据甲、乙两队标书的测算,有三种方案:![]() 甲队单独完成这个工程,刚好如期完成;
甲队单独完成这个工程,刚好如期完成;![]() 乙队单独完成这个工程要比规定时间多用5天;
乙队单独完成这个工程要比规定时间多用5天;![]() **********,剩下的工程由乙队单独做,也正好如期完成. 方案
**********,剩下的工程由乙队单独做,也正好如期完成. 方案![]() 中“星号”部分被损毁了. 已知,一个同学设规定的工期为
中“星号”部分被损毁了. 已知,一个同学设规定的工期为![]() 天,根据题意列出方程:
天,根据题意列出方程:![]()
(1)请将方案中“星号”部分补充出来________________;
(2)你认为哪个方案节省工程款,请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c的对称轴为直线x=1,抛物线与x轴交于A、B两点(点A在点B的左侧),且AB=4,又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与对称轴交于点E,设点P的横坐标为t.
(1)求点A的坐标和抛物线的表达式;
(2)当AE:EP=1:2时,求点E的坐标;
(3)记抛物线的顶点为M,与y轴的交点为C,当四边形CDEM是等腰梯形时,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有分别标有汉字“书”、“ 香”、“ 历”、“ 城”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先搅拌均匀.
(1)若从中任取一个球,球上的汉字刚好是 “书”的概率为__________.
(2)从中任取一球,不放回,再从中任取一球,请用树状图或列表的方法,求取出的两个球上的汉字能组成“历城”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等边三角形,D是边BC上的任意一点,∠ADF=60°,且DF交∠ACE的角平分线于点F.


(1)求证:AC=CD+CF;
(2)如图2,当点D在BC的延长上时,猜想AC、CD、CF的数量关系,并证明你的猜想.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com