练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，一船在海面C处望一灯塔A，是在它的正北方向，另一灯塔B在它的北偏西60°的方向，这船向正西方向航行1海里后到D处，这时灯塔A、B分别在它的东北、西北方向，求这两灯塔间的距离(精确到0.1海里)．

    答案：
    提示：

    提示：过B作BE⊥CD于E，设BE＝x，在Rt△BED和Rt△BCE中，建立方程(1＋x)·tan30°＝x，解为故，在Rt△ABD中，由勾股定理的，AB≈2.4海里．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：中学学习一本通　数学　九年级下册 北师大课标 题型：044

    如图所示，一船在海面C处望见一灯塔A在它的正北方向，另一灯塔B在它的北偏西的方向，此船向正西方向航行l海里后，到达D点，这时灯塔A，B分别在它的东北、西北方向．求这两个灯塔之间的距离．(精确到0.1海里)

    查看答案和解析>>

    科目：初中数学 来源：数学教研室 题型：044

    在某张航海图上，标明了三个观测点的坐标，如图所示，O(0，0)、B(6，0)、C(6、8)，由三个观测点确定的图形区域是海洋生物保护区．

    (1)求圆形区域的面积(p 取3.14)；

    (2)某时刻海面上出现一渔船A，在观测点O测得A位于北偏东45°，同时在观测点B测得A位于北偏东30°，求观测点B到A船的距离(，保留三个有效数字)；

    (3)当渔船A由(2)中位置向正西方向航行时，是否进入海洋生物保护区？通过计算回答．

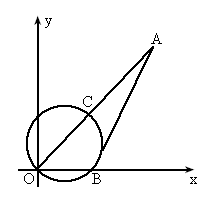
    查看答案和解析>>

    科目：初中数学 来源： 题型：044

    在某张航海图上，标明了三个观测点的坐标，如图所示，O(0，0)、B(6，0)、C(6、8)，由三个观测点确定的图形区域是海洋生物保护区．

    (1)求圆形区域的面积(p 取3.14)；

    (2)某时刻海面上出现一渔船A，在观测点O测得A位于北偏东45°，同时在观测点B测得A位于北偏东30°，求观测点B到A船的距离(，保留三个有效数字)；

    (3)当渔船A由(2)中位置向正西方向航行时，是否进入海洋生物保护区？通过计算回答．

    查看答案和解析>>

    同步练习册答案