证明:(1)如图(1),延长BO交⊙O于点D,连接CD,则
∠D=∠A(同弧或等弧所对的圆周角都相等),
∵OC=OD,
∴∠D=∠OCD,
∵∠BOC=∠D+∠OCD(三角形的一个外角等于与它不相等的两个内角的和),
∴∠BOC=2∠A,
即∠BAC=

∠BOC;

(2)如图(2),延长BO交⊙O于点E,连接CE,则
∠E=∠A(同弧或等弧所对的圆周角都相等),
∵OC=OE,
∴∠E=∠OCE,
∵∠BOC=∠E+∠OCE(三角形的一个外角等于与它不相邻的两个内角的和),
∴∠BOC=2∠A,
即∠BAC=

∠BOC.
分析:(1)延长BO交⊙O于点D,连接CD,根据同弧或等弧所对的圆周角都相等可得∠A=∠D,再根据等腰三角形的两底角相等,∠D=∠OCD,然后利用三角形的外角性质∠BOC=∠D+∠OCD,整理即可得证;
(2)延长BO交⊙O于点E,连接CE,根据同弧或等弧所对的圆周角都相等可得∠A=∠E,再根据等腰三角形的两底角相等,∠E=∠OCE,然后利用三角形的外角性质∠BOC=∠E+∠OCE,整理即可得证;
点评:本题考查了圆周角定理的证明,是基础题,作出辅助线找出与∠BAC相等的角,进行等量代换是解题的关键,方法与定理都需要熟练掌握并灵活运用.

 ∠BOC.
∠BOC.
 ∠BOC;
∠BOC;
 ∠BOC.
∠BOC.

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案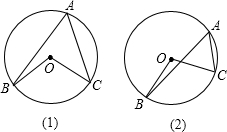
 ∠BOC.
∠BOC.