
科目:初中数学 来源: 题型:解答题
 如图所示的是某别墅的房顶人字架示意图,在△ABC中,AB=10cm,BC=10$\sqrt{3}$cm,BC边上的中线AD=5m.
如图所示的是某别墅的房顶人字架示意图,在△ABC中,AB=10cm,BC=10$\sqrt{3}$cm,BC边上的中线AD=5m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 任意剪一个梯形纸片,利用对折的方法找到两腰的中点E、F,按图中所示的方法过两腰的中点分别将含∠A、∠B的部分向里折,得到两个折痕(如图),沿折痕剪下①②并按图中箭头所指的方向旋转180°,你能得到怎样的四边形?由此,你能说明梯形中位线的性质吗?
任意剪一个梯形纸片,利用对折的方法找到两腰的中点E、F,按图中所示的方法过两腰的中点分别将含∠A、∠B的部分向里折,得到两个折痕(如图),沿折痕剪下①②并按图中箭头所指的方向旋转180°,你能得到怎样的四边形?由此,你能说明梯形中位线的性质吗?查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
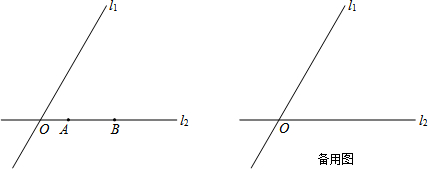
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
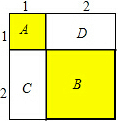 我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.
我们初中数学里的一些代数公式,很多都可以通过表示几何图形面积的方法进行直观推导和解释.例如:平方差公式、完全平方公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com