
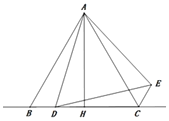
【题目】如图,在△ABC中,AB=AC,AH⊥BC,垂足为H,D为直线BC上一动点(不与点B、C重合),在AD的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
(1)求证:BD=CE;
(2)若点D在线段BC上,问点D运动到何处时,AC⊥DE?请说明理由;
(3)当CE∥AB时,若△ABD中最小角为20°,试探究∠ADB的度数.(直接写出结果,无需写出求解过程)


【答案】(1)证明见解析;(2)当点D运动到BC中点(H点)时,AC⊥DE.理由见解析;(3)∠ADB的度数为20°或40°或100°.
【解析】
(1)由∠DAE=∠BAC证明∠BAD=∠CAE,再证明△BAD≌△CAE即可得到结论,
(2)利用等腰三角形的性质,证明∠CAH=∠CAE,再利用三线合一可得结论,
(3)分三种情形:①当点D在CB的延长线上时,∠ADB=40°; ②当点D在线段BC上时,最小角只能是∠DAB=20°,此时∠ADB=180°-20°-60°=100°. ③当点D在BC 延长线上时,最小角只能是∠ADB=20°;即可得到答案.
证明:(1)如图1.
∵∠DAE=∠BAC
∴∠BAD=∠CAE
在△BAD和△CAE中,
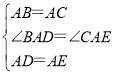 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE.
(2)当点D运动到BC中点(H点)时,AC⊥DE
理由是:如图2.
∵AB=AC,AH⊥BC
∴∠BAH=∠CAH
∵∠BAH=∠CAE,
∴∠CAH=∠CAE
∵AH=AE,
∴AC⊥DE.
(3)∠ADB的度数为20°或40°或100°.
理由如下:
①如图3中,当点D在CB的延长线上时,
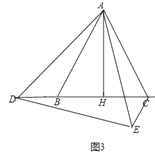
∵CE∥AB,
∴∠BAE=∠AEC,∠BCE=∠ABC.
∵△DAB≌△EAC,
∴∠ADB=∠AEC,∠ABD=∠ACE,
∴∠BAC=∠BAE+∠EAC=∠AEC+∠EAC=180°-∠ACE=180°-∠ABD=∠ABC=∠ACB,∴△ABC是等边三角形,
∴∠ABC=60°
∵△ABD中的最小角是∠BAD=20°,
则∠ADB=∠ABC-∠BAD=40°.
②当点D在线段BC上时,最小角只能是∠DAB=20°,
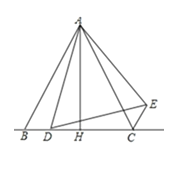
同理可得:∠ADB=180°-20°-60°=100°.
③当点D在BC延长线上时,最小角只能是∠ADB=20°,
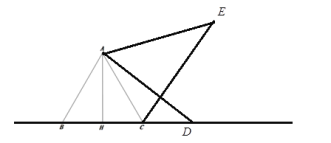
综上所述:满足条件的∠ABD的值为20°或40°或100°.


科目:初中数学 来源: 题型:
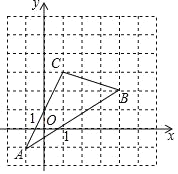
【题目】如图,△ABC在直角坐标系中.
(1)若把△ABC向上平移2个单位,再向右平移2个单位得△A1B1C1,在图中画出△A1B1C1,并写出△A1B1C1的坐标;
(2)求出△ABC的面积S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
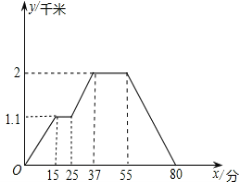
【题目】下图反映的过程是王老师步行从家去书店买书,又去超市买菜, 然后回家.其中x表示时间,y表示王老师离家的距离.根据图象回答下列问题:
(1)书店离王老师家多远?王老师从家到书店用了多少时间?
(2)超市离书店多远?超市离王老师家多远?王老师从超市走回家平均速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级两个班,各选派10名学生参加学校举行的“美丽绍兴乡土风情知识”大赛预赛各参赛选手的成绩如下:
八(1)班:88,91,92,93,93,93,94,98,98,100;
八(2)班:89,93,93,93,95,96,96,98,98,99.
通过整理,得到数据分析表如下:
班级 | 最高分 | 平均分 | 中位数 | 众数 | 方差 |
八(1)班 | 100 | m | 93 | 93 | 12 |
八(2)班 | 99 | 95 | n | 93 | 8.4 |
(1)求表中m、n的值;
(2)依据数据分析表,有同学说:“最高分在(1)班,(1)班的成绩比(2)班好”,但也有同学说(2)班的成绩更好请您写出两条支持八(2)班成绩好的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)在Rt△ABC中,∠BAC=![]() ,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.
,D是BC的中点,E是AD的中点.过点A作AF∥BC交BE的延长线于点F.

(1)求证:△AEF≌△DEB;
(2)证明四边形ADCF是菱形;
(3)若AC=4,AB=5,求菱形ADCFD 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
数学课上,老师让同学们利用三角形纸片进行操作活动,探究有关线段之间的关系.
问题情境:
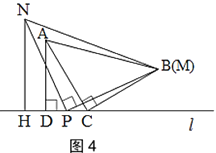
如图1,三角形纸片ABC中,∠ACB=90°,AC=BC.将点C放在直线l上,点A,B位于直线l的同侧,过点A作AD⊥l于点D.
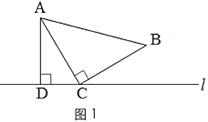
初步探究:
(1)在图1的直线l上取点E,使BE=BC,得到图2.猜想线段CE与AD的数量关系,并说明理由;
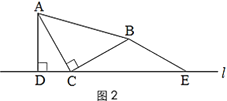
变式拓展:
(2)小颖又拿了一张三角形纸片MPN继续进行拼图操作,其中∠MPN=90°,MP=NP.小颖在图 1 的基础上,将三角形纸片MPN的顶点P放在直线l上,点M与点B重合,过点N作NH⊥l于点 H.
请从下面 A,B 两题中任选一题作答,我选择_____题.
A.如图3,当点N与点M在直线l的异侧时,探究此时线段CP,AD,NH之间的数量关系,并说明理由.
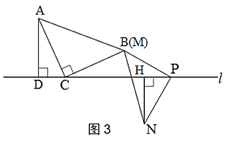
B.如图4,当点N与点M在直线l的同侧,且点P在线段CD的中点时,探究此时线段CD,AD,NH之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有三张正面分别标有数字:-1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中随机抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com