
分析 根据反比例函数的性质和一次函数的性质可以判断选项中的各个函数在其相应的定义域内,y随x是如何变化的,从而可以解答本题.
解答 解:①y=$\frac{1}{x}$,k=1>0,函数图象在第一、三象限,在每个象限象限内y随x的增大而减小,但是在整个象限内不是y随x的增大而减小,故①错误;
②y=-$\frac{1}{x}$,k=-1<0,函数图象在第二、四象限,在每个象限象限内y随x的增大而增大,故②错误;
③y=$\frac{1}{x}$(x>0),k=1>0,函数图象在第一象限内y随x的增大而减小,故③正确;
④y=$\frac{1}{x}$(x<0),k=1>0,函数图象在第三象限内y随x的增大而减小,故④正确;
⑤y=-x+1,k=-1<0,函数图象y随x的增大而减小,故⑤正确;
故答案为:③④⑤.
点评 本题考查反比例函数的性质和一次函数的性质,解题的关键是明确反比例函数和一次函数的性质,尤其是要注意反比例函数说的是在每个象限内,y随x的变化,并不是在整个象限内.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
| A. | .2 | B. | .3 | C. | .4 | D. | .5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,抛物线C:y=mx2+4x+1.
在平面直角坐标系xOy中,抛物线C:y=mx2+4x+1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
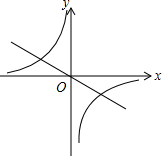 如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象都经过点A(2,-1),若y1>y2,则x的取值范围是( )
如图,正比例函数y1=k1x和反比例函数y2=$\frac{{k}_{2}}{x}$的图象都经过点A(2,-1),若y1>y2,则x的取值范围是( )| A. | -1<x<0 | B. | x>2 | C. | -2<x<0或x>2 | D. | x<-2或0<x<2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
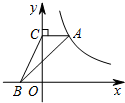 如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AC⊥y轴于点C,点B在x轴上,连结CB、AB.若△ABC的面积为4,则k的值为8.
如图,在平面直角坐标系中,点A在函数y=$\frac{k}{x}$(x>0)的图象上,过点A作AC⊥y轴于点C,点B在x轴上,连结CB、AB.若△ABC的面积为4,则k的值为8.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
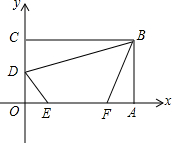 在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )
在平面直角坐标系中,矩形OABC如图所示.点A在x轴正半轴上,点C在y轴正半轴上,且OA=6,OC=4,D为OC中点,点E、F在线段OA上,点E在点F左侧,EF=2.当四边形BDEF的周长最小时,点E的坐标是( )| A. | ($\frac{1}{2}$,0) | B. | ($\frac{4}{3}$,0) | C. | ($\frac{3}{2}$,0) | D. | (2,0) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
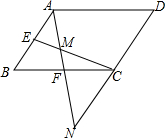 如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.
如图,在?ABCD中,E、F分别为AB、BC的中点,连接EC、AF,AF与EC交于点M,AF的延长线与DC的延长线交于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com