
����Ŀ����ѧ�����У����ͳ�Ļ�������,ijУ�����ˡ�Χ�����š�����ʫ�躺�֡�������īƮ�㡱����ʷѧ���䡱������չ�Σ�ÿλѧ��������ֻѡ����һ�ţ�.
��1��ѧУ���꼶����ѧ������ѡ�ε��飬
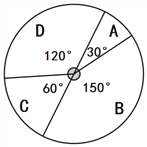

�õ���ͼ��ʾ��ͳ��ͼ������Ƹ�У���꼶420��ѧ��ѡ��ʫ�躺�֡���������
(2)����īƮ�㡱�黭��ļס��ҡ������˵��鷨ˮƽ�൱��ѧУ������������ͬѧ����ѡ�����μ����鷨����������ұ�ѡ�еĸ��ʣ���Ҫ���б�����״ͼ��

| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������Ϊ����ӡˢ��˾�����ӡˢ��Ƭ�Ƽ۷�ʽ��˵�������ȴ������ӡˢ��˾���һ��ĸ�ڿ�Ƭ��ӡˢ�����ٽ���Ƭ��ÿ��15Ԫ�ļ۸��ۣ��������������۵��ɱ����ҳɱ�ֻ������Ʒ���ӡˢ�ѣ�����������ӡ�����ſ�Ƭ���ſ�ʹ�ÿ�Ƭȫ���۳���������ɱ���2�ɣ��� ��

A. 112 B. 121 C. 134 D. 143
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ����AM��BN�ǡ�O���������ߣ�EΪ��O��һ�㣬����E��ֱ��DC�ֱ�AM��BN�ڵ�D��C����CB=CE��
��1����֤��DA=DE��
��2����AB=6��CD=4![]() ����ͼ����Ӱ���ֵ������
����ͼ����Ӱ���ֵ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������7�֣���ͼ����B��F��C��E��һ��ֱ���ϣ�FB=CE��AC=DF���������������������AB=DE���ڡ�A=��D���ۡ�ACB=��DFE��ѡ��һ�����ʵ�������ʹAB��ED������������֤����
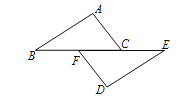
��1��ѡ��������� ������ţ�
��2��֤����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c����A����1��0����B��3��0����N��2��3�����㣬����y�ύ�ڵ�C��
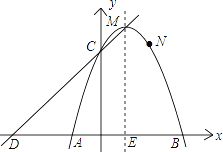
��1����������κ����Ľ���ʽ����д������M����C�����ꣻ
��2����ֱ��y=kx+d����C��M���㣬����x�ύ�ڵ�D����֤���ı���CDAN��ƽ���ı��Σ�
��3����P��������κ����ĶԳ�����һ���㣬��̽�����Ƿ���������ĵ�P��ʹ�Ե�PΪԲ�ĵ�Բ����A��B���㣬������ֱ��CD���У�������ڣ��������P�����ꣻ��������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������װ�����·���Ԫ���ڼ䵽�̳�������䡢���ӻ���ϴ�»������ҵ磬�պø��̳��Ƴ������Żݻ�������Ż�������±���
�����ԭ�ۣ� | �ۿ��Ż� |
������3000Ԫ�IJ��� | ���ۿ��Ż� |
����3000Ԫ��������10000Ԫ���� | �����ۣ� |
����10000Ԫ�IJ��� | ���� |
����ʱ�����������ܵ���������2000Ԫ����160Ԫ�Ż� | |
�磺��ԭ��5000Ԫ����Ʒ��ʵ�ʻ��ѣ�
![]() ��Ԫ��
��Ԫ��
��1����֪���Ź�����������ҵ�ԭ�ۺϼ�Ϊ11500Ԫ�����һ����֧�������������ʵ�ʻ��ѣ�
��2������ڸ��̳�����һ��ԭ��Ϊ![]() Ԫ����Ʒ��
Ԫ����Ʒ��![]() �������ú�
�������ú�![]() �Ĵ���ʽ��ʾʵ�ʻ��ѣ�
�Ĵ���ʽ��ʾʵ�ʻ��ѣ�
��3������ǰ������ͻȻ�뵽�����һ����֧������Ȼ�ۿ��Żݸ���ȴֻ������һ������160Ԫ�Żݣ�������������ҵ�ֿ�֧�����������ϲ�֧������һ������֧�����Ϳ������ܶ������160Ԫ�Żݣ���֪���Ź���ı���ԭ��4800Ԫ�����ӻ�ԭ��4600Ԫ��ϴ�»�ԭ��2100Ԫ������ͨ�������������Ƴ����Żݵ�֧��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����߳�Ϊ12 cm��������ABCD����Խ���AC�������ٰ�ABC����AD����ƽ�ƣ��õ���A��B��C�����������������ص����ֵ����Ϊ32 cm2�������ƶ��ľ���AA������( )
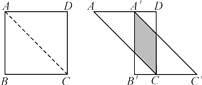
A. 4 cm B. 8 cm C. 6 cm D. 4 cm��8 cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�������ABC�У�D��E�ֱ���AB��AC���ϵĵ㣬��ADC�ա�ADC�䣬��AEB�ա�AEB������C��D��EB���BC��BE��CD���ڵ�F������BAC=35��������BFC�Ĵ�С�ǣ�������

A. 105�� B. 110�� C. 100�� D. 120��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��EF��AD����1=��2����B=55�������BDG�Ĵ�С��
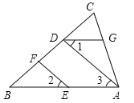
��ͬѧ��������ĺ����ϰѽ����̲���������
�⣺�� EF//AD��������(��֪)
�ࡡ��2=��3�� (����������������������)
�֡ߡ���1=��2�� (��֪)
�ࡡ��1=��3�� (��������)
�ࡡ����������������(�ڴ�����ȣ���ֱ��ƽ��)
�ࡡ��B����BDG=180���� (������������������������)
�ߡ���B=55��������(��֪)
�ࡡ��BDG =����������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com