
 如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中:
如图,六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则下列结论中:分析 根据相似多边形对应角相等可对①进行判断;根据相似多边形对应边之比、周长之比等于相似比,而面积之比等于相似比的平方可对②③④进行判断.
解答 解:由于六边形ABCDEF∽六边形GHIJKL,则∠E=∠K,所以①错误;
六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则BC:HI=2:1,所以②正确;
由于六边形ABCDEF∽六边形GHIJKL,相似比为2:1,则六边形ABCDEF的周长:六边形GHIJKL的周长=2:1,S六边形ABCDEF=4S六边形GHIJKL,所以③④错误;
故答案为②.
点评 本题考查了相似多边形的性质:对应角相等;对应边的比相等;相似多边形对应边的比叫做相似比,相似多边形周长之比等于相似比,而面积之比等于相似比的平方.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:填空题
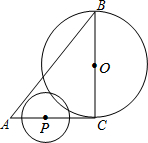 如图,Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O是以BC边为直径的圆,点P为AC边上动点,⊙P的半径为2.设AP=x,则当x的取值范围是6-2$\sqrt{5}$<x≤6时,⊙P与⊙O相交.
如图,Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O是以BC边为直径的圆,点P为AC边上动点,⊙P的半径为2.设AP=x,则当x的取值范围是6-2$\sqrt{5}$<x≤6时,⊙P与⊙O相交.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
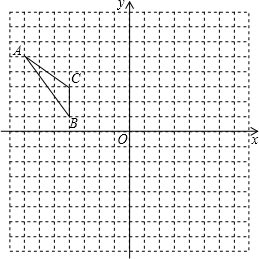 如图所示,在平面直角坐标系中有一个△ABC,且点B的坐标是(-4,1).
如图所示,在平面直角坐标系中有一个△ABC,且点B的坐标是(-4,1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
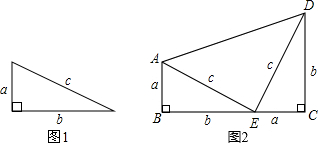 【定理表述】
【定理表述】查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
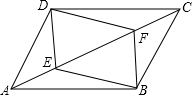 已知:如图,四边形ABCD是平行四边形,DE⊥AC,BF⊥AC,垂足分别是E、F.连结BE、DF.四边形DEBF是什么特殊的四边形?请说明理由.
已知:如图,四边形ABCD是平行四边形,DE⊥AC,BF⊥AC,垂足分别是E、F.连结BE、DF.四边形DEBF是什么特殊的四边形?请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com