
分析 M、N两点关于对角线AC对称,所以DM=BN,进而求出CN的长度.再由勾股定理求得DN,sin∠ADN=cos∠CDN=$\frac{CD}{DN}$.
解答 解:在正方形ABCD中,AB=CD.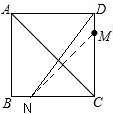
∵M、N两点关于对角线AC对称,
∴BN=DM=1.
又∵sin∠ADN=sin(90°-∠CDN)=cos∠CDN,
∵CN=BC-BN=3-1=2,CD=3,
∴DN=$\sqrt{{CN}^{2}{+CD}^{2}}$=$\sqrt{{2}^{2}{+3}^{2}}$=$\sqrt{13}$,
∴sin∠ADN=cos∠CDN=$\frac{CD}{DN}$=$\frac{3}{\sqrt{13}}$=$\frac{3\sqrt{13}}{13}$,
故答案为:$\frac{3\sqrt{13}}{13}$.
点评 本题综合考查了正方形的性质,轴对称的性质以及锐角三角函数的定义,关键是得出sin∠ADN=cos∠CDN=$\frac{CD}{DN}$.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:填空题
 如图,在矩形ABCD中,BC=2,M为对角线BD的中点,连接CM,以CM为直径作⊙O交BD于点E,连接AE,当直线AE与⊙O相切时,AB的长为$\sqrt{6}$-$\sqrt{2}$.
如图,在矩形ABCD中,BC=2,M为对角线BD的中点,连接CM,以CM为直径作⊙O交BD于点E,连接AE,当直线AE与⊙O相切时,AB的长为$\sqrt{6}$-$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
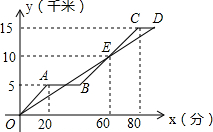 小明与小英同时从人们广场出发,沿同一路线骑自行车匀速前往净月潭公园,小明骑行20分钟后因事耽误一会儿,事后继续按原速骑行到达目的地.在小明和小英骑行过程中,二人骑行的路程y(千米)与小英的骑行时间x(分)之间的函数图象如图所示.
小明与小英同时从人们广场出发,沿同一路线骑自行车匀速前往净月潭公园,小明骑行20分钟后因事耽误一会儿,事后继续按原速骑行到达目的地.在小明和小英骑行过程中,二人骑行的路程y(千米)与小英的骑行时间x(分)之间的函数图象如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
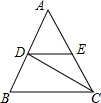 如图,在△ABC中,∠ACB的平分线交AB于点D,点E在AC上,DE∥BC,若∠CDE=30°,则∠AED=( )
如图,在△ABC中,∠ACB的平分线交AB于点D,点E在AC上,DE∥BC,若∠CDE=30°,则∠AED=( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com