
分析 根据相反数得出方程,根据偶次方和算术平方根的非负性得出x+3=0,x-y-4=0,求出x、y,求出xy,求出$\sqrt{xy}$的整数部分,最后根据平方根定义求出即可.
解答 解:根据题意得:2014(x+3)2+$\frac{{\sqrt{x-y-4}}}{{{{2015}^2}}}$=0,
x+3=0,x-y-4=0,
解得:x=-3,y=-7,
xy=21,
∵4<$\sqrt{21}$<5,
∴$\sqrt{xy}$的整数部分为4,
∴$\sqrt{xy}$的整数部分的平方根是±2.
点评 本题考查了算术平方根、平方根、估算无理数的大小、绝对值和算术平方根的非负性等知识点,能熟记每个知识点是解此题的关键.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:解答题
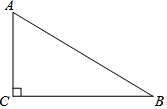 如图,在Rt△ABC中,∠ACB=90°.
如图,在Rt△ABC中,∠ACB=90°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com