
【题目】如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以4cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以3cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了 s时,以C点为圆心,2cm为半径的圆与直线EF相切.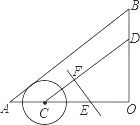
【答案】![]()
【解析】解:当以点C为圆心,2cm为半径的圆与直线EF相切时,
此时,CF=2,
由题意得:AC=4t,BD=3t
∴OC=8﹣4t,OD=6﹣3t,
∵点E是OC的中点,
∴CE= ![]() OC=4﹣2t,
OC=4﹣2t,
∵∠EFC=∠O=90°,∠FCE=∠DCO
∴△EFC∽△DOC
∴ ![]() =
= ![]()
∴EF= ![]() =
= ![]()
由勾股定理可知:CE2=CF2+EF2 ,
∴(4﹣2t)2=2 2+( ![]() )2 ,
)2 ,
解得:t= ![]() 或t=
或t= ![]() ,
,
∵0≤t≤2,
∴t= ![]() .
.
故答案为: ![]() .
.
由题意可设AC=4t,BD=3t,以点C为圆心,2cm为半径的圆与直线EF相切,根据切线的性质可得∠EFC=∠O=90°,即可证△EFC∽△DOC,由相似三角形的性质可得![]() =
= ![]() ,可求EF的长,在直角三角形CEF中用勾股定理可得关于t的值。
,可求EF的长,在直角三角形CEF中用勾股定理可得关于t的值。


科目:初中数学 来源: 题型:
【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1: ![]() ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.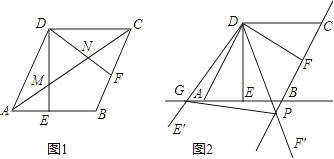
(1)如图1,连接AC分别交DE、DF于点M、N,求证:MN= ![]() AC;
AC;
(2)如图2,将△EDF以点D为旋转中心旋转,其两边DE′、DF′分别与直线AB、BC相交于点G、P,连接GP,当△DGP的面积等于3 ![]() 时,求旋转角的大小并指明旋转方向.
时,求旋转角的大小并指明旋转方向.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,某公司有三个住宅区,A、B、C各区分别住有职工30人,15人,10人,且这三点在一条大道上(A,B,C三点共线),已知AB=100米,BC=200米.为了方便职工上下班,该公司的接送车打算在此间只设一个停靠点,为使所有的人步行到停靠点的路程之和最小,那么该停靠点的位置应设在( )
![]()
A. 点AB. 点BC. A,B之间D. B,C之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.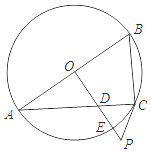
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司开发出一款新的节能产品,该产品的成本价为6元/件,该产品在正式投放市场前通过代销点进行了为期一个月(30天)的试营销,售价为8元/件,工作人员对销售情况进行了跟踪记录,并将记录情况绘成图象,图中的折线ODE表示日销售量y(件)与销售时间x(天)之间的函数关系,已知线段DE表示的函数关系中,时间每增加1天,日销售量减少5件. 
(1)第24天的日销售量是件,日销售利润是元.
(2)求y与x之间的函数关系式,并写出x的取值范围;
(3)日销售利润不低于640元的天数共有多少天?试销售期间,日销售最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,数轴上的点A,B,C,D表示的数分别为:-1.5,-3,2,3.5.
![]()
(1)将A,B,C,D表示的数按从小到大的顺序用“<”号连接起来;
(2)若将原点改在C点,其余各点所对应的数分别为多少?将这些数按从小到大的顺序用“<”连接起来;
(3)改变原点位置后,点A,B,C,D所表示的数大小顺序改变了吗?这说明了数轴的什么性质?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com