
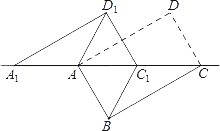
【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,连结AD1,BC1.若∠ACB=30°,AB=1,CC1=x,△ACD与△A1C1D1重叠部分的面积为s,则下列结论:①△A1AD1≌△CC1B②当x=1时,四边形ABC1D1是菱形 ③当x=2时,△BDD1为等边三角形 ④s=![]() (x﹣2)2(0<x<2),其中正确的有( )
(x﹣2)2(0<x<2),其中正确的有( )
A. 1 个B. 2 个C. 3 个D. 4 个
【答案】C
【解析】
①正确,根据SSS即可判断;
②正确,证明四边相等即可解决问题;
③正确,只要证明BD=DD1,∠BDD1=60°即可;
④错误,利用三角形的面积公式计算即可判定;
解:∵AC=A1C1,
∴AA1=CC1
∵BC=D1A1,∠AA1D1=∠BCC1,
∴△A1AD1≌△CC1B,故①正确,
在Rt△ABC中,∵∠ACB=30°,AB=1,
∴AC=A1C1=2,
当x=1时,AC1=CC1=1,
∴AC1=AB,
∵∠BAC=60°,
∴△ABC1是等边三角形,
同法可证:△AD1C1是等边三角形,
∴AB=BC1=AC1=AD1=C1D1,
∴四边形ABC1D1是菱形,故②正确,
当x=2时,BD=AC=2,DD1=2,∠BDD1=60°,
∴△BDD1是等边三角形,故③正确,
当0<x<2时,S=![]()
![]() (2﹣x)
(2﹣x)![]() (2﹣x)=
(2﹣x)=![]() (2﹣x)2,故④错误.
(2﹣x)2,故④错误.
故选:C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
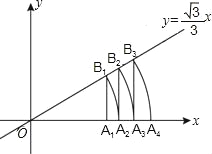
【题目】如图,直线![]() x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为______,点An______.
x,点A1坐标为(1,0),过点A1作x轴的垂线交直线于点B1,以原点O为圆心,OB1长为半径画弧交x轴于点A2;再过点A2作x轴的垂线交直线于点B2,以原点O为圆心,OB2长为半径画弧交x轴于点A3,…,按此做法进行下去,点A4的坐标为______,点An______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l:y=﹣x+4,在直线l上取点B1,过B1分别向x轴,y轴作垂线,交x轴于A1,交y轴于C1,使四边形OA1B1C1为正方形;在直线l上取点B2,过B2分别向x轴,A1B1作垂线,交x轴于A2,交A1B1于C2,使四边形A1A2B2C2为正方形;按此方法在直线l上顺次取点B3,B4,…,Bn,依次作正方形A2A3B3C3,A3A4B4C4,…,An﹣1AnBnCn,则A3的坐标为___,B5的坐标为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八(1)班同学为了解2018年姜堰某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,请解答以下问题:
月均用水量x(t) | 频数(户) | 频率 |
0<x≤5 | 6 | 0.12 |
5<x≤10 | 12 | 0.24 |
10<x≤15 | m | 0.32 |
15<x≤20 | 10 | n |
20<x≤25 | 4 | 0.08 |
25<x≤30 | 2 | 0.04 |
(1)本次调查采用的调杳方式是 (填“普査”或“抽样调查”),样本容量是 ;
(2)补全频数分布直方图:
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“15<x≤20”的圆心角度数是 ;
(4)若该小区有5000户家庭,求该小区月均用水量超过20t的家庭大约有多少户?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=AC,BC=20,DE是△ABC的中位线,点M是边BC上一点,BM=3,点N是线段MC上的一个动点,连接DN,ME,DN与ME相交于点O.若△OMN是直角三角形,则DO的长是______.

查看答案和解析>>
科目:初中数学 来源: 题型:
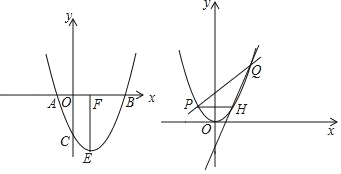
【题目】抛物线y=x2+bx+c经过点A、B、C,已知A(﹣1,0),C(0,﹣3).
(1)求抛物线的解析式;
(2)如图1,抛物线顶点为E,EF⊥x轴于F点,M(m,0)是x轴上一动点,N是线段EF上一点,若∠MNC=90°,请指出实数m的变化范围,并说明理由.
(3)如图2,将抛物线平移,使其顶点E与原点O重合,直线y=kx+2(k>0)与抛物线相交于点P、Q(点P在左边),过点P作x轴平行线交抛物线于点H,当k发生改变时,请说明直线QH过定点,并求定点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
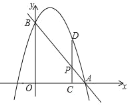
【题目】如图,已知直线y=﹣x+4分别交x轴、y轴于点A、B,抛物线过y=ax2+bx+c经过A,B两点,点P是线段AB上一动点,过点P作PC⊥x轴于点C,交抛物线于点D.
(1)若抛物线的解析式为y=﹣![]() x2+x+4,设其顶点为M,其对称轴交AB于点N.
x2+x+4,设其顶点为M,其对称轴交AB于点N.
①求点M、N的坐标;
②是否存在点P,使四边形MNPD为菱形?并说明理由;
(2)当点P的横坐标为2时,是否存在这样的抛物线,使得以B、P、D为顶点的三角形是直角三角形?若存在,求出满足条件的抛物线的解析式;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在倡导学生大课间活动中,随机抽取了部分学生对“我最喜爱课间活动”进行了一次抽样调查,分别从打篮球、踢足球、自由活动、跳绳、其它、等5个方面进行问卷调查(每人只能选一项),根据调查结果绘制了如图的不完整统计图,请你根据图中信息,解答下列问题
(1)本次调查共抽取了学生多少人?
(2)求本次调查中喜欢踢足球人数,并补全条形统计图;
(3)若全校共有中学生1200人,请你估计我校喜欢跳绳学生有多少人.

查看答案和解析>>
科目:初中数学 来源: 题型:
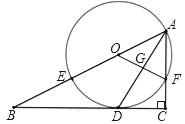
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=![]() ,求DG的长,
,求DG的长,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com