
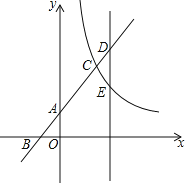
【题目】如图所示,直线y=x+2与坐标轴交于A、B两点,与反比例函数y=![]() (x>0)交于点C,已知AC=2AB.
(x>0)交于点C,已知AC=2AB.
(1)求反比例函数解析式;
(2)若在点C的右侧有一平行于y轴的直线,分别交一次函数图象与反比例函数图象于D、E两点,若CD=CE,求点D坐标.
【答案】(1)y=![]() ;(2)D(6,8).
;(2)D(6,8).
【解析】
(1)作CM⊥y轴于M,如图,利用直线解析式确定A(0,2),B(﹣2,0),再根据平行线分线段成比例定理求出MC=4,AM=4,则C(4,6),然后把C点坐标代入y=![]() 中求出k得到反比例函数解析式;
中求出k得到反比例函数解析式;
(2)MC交直线DE于N,如图,证明△CND为等腰直角三角形得到CN=DN,再利用CD=CE得到CN=NE=DN,设CN=t,则N(4+t,6),D(4+t,6+t),E(4+t,6﹣t),然后把E(4+t,6﹣t)代入y=![]() 得(4+t)(6﹣t)=24,最后解方程求出t得到D点坐标.
得(4+t)(6﹣t)=24,最后解方程求出t得到D点坐标.
解:(1)作CM⊥y轴于M,如图,
当x=0时,y=x+2=2,则A(0,2),
当y=0时,x+2=0,解得x=﹣2,则B(﹣2,0),
∵MC∥OB,
∴![]() =
=![]() =
=![]() =2,
=2,
∴MC=2OB=4,AM=2OA=4,
∴C(4,6),
把C(4,6)代入y=![]() 得k=4×6=24,
得k=4×6=24,
∴反比例函数解析式为y=![]() ;
;
(2)MC交直线DE于N,如图,
∵MC=MA,
∴△MAC为等腰直角三角形,
∴∠ACM=45°,
∴∠DCN=45°,
∴△CND为等腰直角三角形,
∴CN=DN,
∵CD=CE,
∴CN=NE=DN,
设CN=t,则N(4+t,6),D(4+t,6+t),E(4+t,6﹣t),
把E(4+t,6﹣t)代入y=![]() 得(4+t)(6﹣t)=24,解得t1=0(舍去),t2=2,
得(4+t)(6﹣t)=24,解得t1=0(舍去),t2=2,
∴D(6,8).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AB=1,tanC=![]() ,以点A为圆心,AB长为半径作弧交AC于D,分别以B、D为圆心,以大于
,以点A为圆心,AB长为半径作弧交AC于D,分别以B、D为圆心,以大于![]() BD长为半径作弧,两弧交于点E,射线AE与BC于F,过点F作FG⊥AC于G,则FG的长为______.
BD长为半径作弧,两弧交于点E,射线AE与BC于F,过点F作FG⊥AC于G,则FG的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】风筝又称“纸鸢”、“鸢儿”,放风筝是民间传统游戏之一,也是清明时节人们所喜爱的活动.小李打算抓住这一机遇,以每个20元的成本制作了30个风筝,再以每个40元的价格售出,很快就被一抢而空,于是小李计划加紧制作第二批风筝.
(1)预计第二批风筝的成本是每个15元,仍以原价出售,若两批风筝的总利润不低于2850元,则第二批至少应该制作多少个风筝?
(2)在实际制作过程中,小李按照(1)中风筝的最低数量进行制作,但制作风筝的成本比预期的15元多了a%(a>10),于是小李决定将售价也提高a%,附近的商户受到小李的启发,也纷纷卖起了风筝,在市场冲击下,小李实际还剩下![]() a%的风筝没卖出去,但仍然比第一次获利多1668元,求a的值.
a%的风筝没卖出去,但仍然比第一次获利多1668元,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是![]() =0.4,
=0.4,![]() =0.6,则甲的射击成绩较稳定
=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】边长为4的正方形AOBC在坐标系中的位置如图所示,若OB边保持不动,推动AOBC向右倾斜30°得四边形DOBE,则点E的坐标为( )
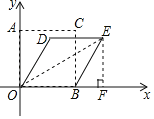
A.(5,4)B.(6,2![]() )C.(6,3
)C.(6,3![]() )D.(4+2
)D.(4+2![]() ,5)
,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
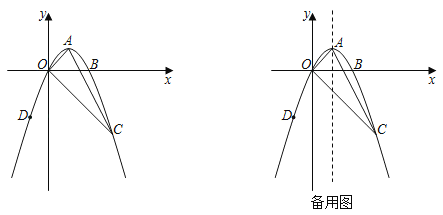
【题目】已知抛物线y=ax2+bx+c与x轴交于O、B两点,其顶点A坐标为(1,1),点C为抛物线在第四象限内的一点,其坐标为(3,﹣3).
(1)求抛物线解析式;
(2)点D为抛物线在第三象限内的一点,过点D向x轴作垂线段,垂足为H,是否存在点D使得△DHO与△AOC相似,如果存在,请求出点D坐标,如果不存在,请说明理由;
(3)点E、F分别为抛物线以及抛物线对称轴上的两动点,请问是否存在以BO为边,B、O、E、F为顶点的平行四边形,如果存在请直接写出点E坐标,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
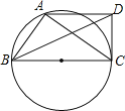
【题目】 若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
(1)已知△ABC是比例三角形,AB=2,BC=3,请直接写出所有满足AC条件的长;
(2)如图,点A在以BC为直径的圆上,BD平分∠ABC,AD∥BC,∠ADC=90°.
①求证:△ABC为比例三角形;
②求![]() 的值.
的值.
(3)若以点C为顶点的抛物线y=mx2-4mx-12m(m<0)与x轴交于A、B两点,△ABC是比例三角形,若点M(x0,y0)为该抛物线上任意一点,总有n-![]() ≤-
≤-![]() my02-40
my02-40![]() y0+298成立,求实数n的最大值.
y0+298成立,求实数n的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AD=6,E为AB的中点,将△ADE沿DE翻折得到△FDE,延长EF交BC于G,FH⊥BC,垂足为H,延长DF交BC与点M,连接BF、DG.以下结论:①∠BFD+∠ADE=180°;②△BFM为等腰三角形;③△FHB∽△EAD;④BE=2FM⑤S△BFG=2.6 ⑥sin∠EGB=![]() ;其中正确的个数是( )
;其中正确的个数是( )

A.3B.4C.5D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com