
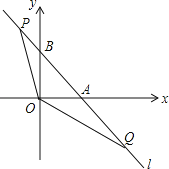
ЁОЬтФПЁПШчЭМЃЌжБЯпlЃКy=Љx+1гыxжсЃЌyжсЗжБ№НЛгкAЃЌBСНЕуЃЌЕуPЃЌQЪЧжБЯпlЩЯЕФСНИіЖЏЕуЃЌЧвЕуPдкЕкЖўЯѓЯоЃЌЕуQдкЕкЫФЯѓЯоЃЌЁЯPOQ=135ЁуЃЎ
ЃЈ1ЃЉЧѓЁїAOBЕФжмГЄЃЛ
ЃЈ2ЃЉЩшAQ=tЃО0ЃЌЪдгУКЌtЕФДњЪ§ЪНБэЪОЕуPЕФзјБъЃЛ
ЃЈ3ЃЉЕБЖЏЕуPЃЌQдкжБЯпlЩЯдЫЖЏЕНЪЙЕУЁїAOQгыЁїBPOЕФжмГЄЯрЕШЪБЃЌМЧtanЁЯAOQ=mЃЌШєЙ§ЕуAЕФЖўДЮКЏЪ§y=ax2+bx+cЭЌЪБТњзувдЯТСНИіЬѕМўЃК
Ђй6a+3b+2c=0ЃЛ
ЂкЕБmЁмxЁмm+2ЪБЃЌКЏЪ§yЕФзюДѓжЕЕШгк![]() ЃЌЧѓЖўДЮЯюЯЕЪ§aЕФжЕЃЎ
ЃЌЧѓЖўДЮЯюЯЕЪ§aЕФжЕЃЎ
ЁОД№АИЁП(1) ЁїAOBжмГЄЮЊ2+![]() ЃЎ(2) PЃЈЉ
ЃЎ(2) PЃЈЉ![]() ЃЌ1+
ЃЌ1+![]() ЃЉЃЎ(3) aЕФжЕЮЊ
ЃЉЃЎ(3) aЕФжЕЮЊ![]() ЛђЉ2
ЛђЉ2![]() Љ2ЃЎ
Љ2ЃЎ
ЁОНтЮіЁП
ЪдЬтЗжЮіЃКЃЈ1ЃЉЯШЧѓГіAЁЂBзјБъЃЌдйЧѓГіOBЁЂOAЁЂABМДПЩНтОіЮЪЬтЃЎЃЈ2ЃЉгЩЁїPBOЁзЁїOAQЃЌЕУ![]() =
=![]() ЃЌЧѓГіPBЃЌдйИљОнЕШбќжБНЧШ§НЧаЮаджЪПЩвдЧѓЕУЕуPзјБъЃЎЃЈ3ЃЉЯШЧѓГіmЕФжЕЃЌЗжЂйaЃО0ЃЌЂкaЃМ0ЃЌСНжжЧщаЮЃЌРћгУЖўДЮКЏЪ§аджЪЗжБ№ЧѓНтМДПЩЃЎ
ЃЌЧѓГіPBЃЌдйИљОнЕШбќжБНЧШ§НЧаЮаджЪПЩвдЧѓЕУЕуPзјБъЃЎЃЈ3ЃЉЯШЧѓГіmЕФжЕЃЌЗжЂйaЃО0ЃЌЂкaЃМ0ЃЌСНжжЧщаЮЃЌРћгУЖўДЮКЏЪ§аджЪЗжБ№ЧѓНтМДПЩЃЎ
ЪдЬтНтЮіЃКЃЈ1ЃЉдкКЏЪ§y=Љx+1жаЃЌСюx=0ЃЌЕУy=1ЃЌ
ЁрBЃЈ0ЃЌ1ЃЉЃЌ
Сюy=0ЃЌЕУx=1ЃЌ
ЁрAЃЈ1ЃЌ0ЃЉЃЌ
дђOA=OB=1ЃЌAB=![]() ЃЌ
ЃЌ
ЁрЁїAOBжмГЄЮЊ1+1+![]() =2+
=2+![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЁпOA=OBЃЌ
ЁрЁЯABO=ЁЯBAO=45ЁуЃЌ
ЁрЁЯPBO=ЁЯQAO=135ЁуЃЌ
ЩшЁЯPOB=xЃЌдђЁЯOPB=ЁЯAOQ=135ЁуЉxЉ90Ёу=45ЁуЉxЃЌ
ЁрЁїPBOЁзЁїOAQЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
ЁрPB=![]() =
=![]() ЃЌ
ЃЌ
Й§ЕуPзїPHЁЭOBгкHЕуЃЌ
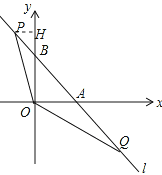
дђЁїPHBЮЊЕШбќжБНЧШ§НЧаЮЃЌ
ЁпPB=![]() ЃЌ
ЃЌ
ЁрPH=HB=![]() ЃЌ
ЃЌ
ЁрPЃЈЉ![]() ЃЌ1+
ЃЌ1+![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉгЩЃЈ2ЃЉПЩжЊЁїPBOЁзЁїOAQЃЌШєЫќУЧЕФжмГЄЯрЕШЃЌдђЯрЫЦБШЮЊ1ЃЌМДШЋЕШЃЌ
ЁрPB=AQЃЌ
Ёр![]() =tЃЌ
=tЃЌ
ЁпtЃО0ЃЌ
Ёрt=1ЃЌ
ЭЌРэПЩЕУQЃЈ1+![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌ
ЃЉЃЌ
Ёрm=![]() =
=![]() Љ1ЃЌ
Љ1ЃЌ
ЁпХзЮяЯпОЙ§ЕуAЃЌ
Ёрa+b+c=0ЃЌ
гжЁп6a+3b+2c=0ЃЌ
Ёрb=Љ4aЃЌc=3aЃЌ
ЖдГЦжсx=2ЃЌШЁжЕЗЖЮЇ![]() Љ1Ёмx
Љ1Ёмx![]() +1ЃЌ
+1ЃЌ
ЂйШєaЃО0ЃЌдђПЊПкЯђЩЯЃЌ
гЩЬтвтx=![]() Љ1ЪБШЁЕУзюДѓжЕ
Љ1ЪБШЁЕУзюДѓжЕ![]() =2
=2![]() +2ЃЌ
+2ЃЌ
МДЃЈ![]() Љ1ЃЉ2a+ЃЈ
Љ1ЃЉ2a+ЃЈ![]() Љ1ЃЉb+c=2
Љ1ЃЉb+c=2![]() +2ЃЌ
+2ЃЌ
НтЕУa=![]() ЃЎ
ЃЎ
ЂкШєaЃМ0ЃЌдђПЊПкЯђЯТЃЌ
гЩЬтвтx=2ЪБШЁЕУзюДѓжЕ2![]() +2ЃЌ
+2ЃЌ
МД4a+2b+c=2![]() +2ЃЌ
+2ЃЌ
НтЕУa=Љ2![]() Љ2ЃЎ
Љ2ЃЎ
злЩЯЫљЪіЫљЧѓaЕФжЕЮЊ![]() ЛђЉ2
ЛђЉ2![]() Љ2ЃЎ
Љ2ЃЎ


 ЭЈГЧбЇЕфФЌаДФмЪжЯЕСаД№АИ
ЭЈГЧбЇЕфФЌаДФмЪжЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСавЛдЊЖўДЮЗНГЬжаУЛгаЪЕЪ§ИљЕФЗНГЬЪЧЃЈЁЁЁЁЃЉ
A. ЃЈxЉ1ЃЉ2ЃН1 B. x2+2xЉ10ЃН0 C. x2+4ЃН7 D. x2+x+1ЃН0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
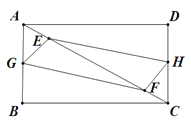
ЁОЬтФПЁПЫФБпаЮABCD жаЃЌAB=3ЃЌBC=4ЃЌEЃЌF ЪЧЖдНЧЯп ACЩЯЕФСНИіЖЏЕуЃЌЗжБ№Дг AЃЌC ЭЌЪБГіЗЂЃЌ ЯрЯђЖјааЃЌЫйЖШОљЮЊ 1cm/sЃЌдЫЖЏЪБМфЮЊ t УыЃЌЕБЦфжавЛИіЖЏЕуЕНДяКѓОЭЭЃжЙдЫЖЏЃЎ
ЃЈ1ЃЉШє GЃЌH ЗжБ№ЪЧ ABЃЌDC жаЕуЃЌЧѓжЄЃКЫФБпаЮ EGFH ЪМжеЪЧЦНааЫФБпаЮЃЎ
ЃЈ2ЃЉдкЃЈ1ЃЉЬѕМўЯТЃЌЕБ t ЮЊКЮжЕЪБЃЌЫФБпаЮ EGFH ЮЊОиаЮЃЎ
ЃЈ3ЃЉШє GЃЌH ЗжБ№ЪЧелЯп AЉBЉCЃЌCЉDЉA ЩЯЕФЖЏЕуЃЌгы EЃЌF ЯрЭЌЕФЫйЖШЭЌЪБГіЗЂЃЌЕБ t ЮЊКЮжЕЪБЃЌЫФБпаЮ EGFH ЮЊСтаЮЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
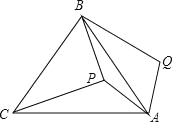
ЁОЬтФПЁПШчЭМЃЌPЪЧЕШБпШ§НЧаЮABCФквЛЕуЃЌНЋЯпЖЮAPШЦЕуAЫГЪБеыа§зЊ60ЁуЕУЕНЯпЖЮAQЃЌСЌНгBQЃЎШєPA=6ЃЌPB=8ЃЌPC=10ЃЌдђЫФБпаЮAPBQЕФУцЛ§ЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШєЖўДЮКЏЪ§yЃН2x2Љ4kx+1ЃЎЕБxЁмlЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЌдђkЕФШЁжЕЗЖЮЇЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
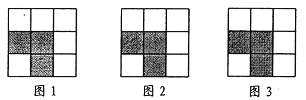
ЁОЬтФПЁПЯТСа3ЁС3ЭјИёЖМЪЧгЩ9ИіЯрЭЌаЁе§ЗНаЮзщГЩЃЌУПИіЭјИёЭМжага3ИіаЁе§ЗНаЮвбЭПЩЯвѕгАЃЌЧыдкгрЯТЕФ6ИіПеАзаЁе§ЗНаЮжаЃЌАДЯТСавЊЧѓЭПЩЯвѕгАЃК
ЃЈ1ЃЉбЁШЁ1ИіЭПЩЯвѕгАЃЌЪЙ4ИівѕгАаЁе§ЗНаЮзщГЩвЛИіжсЖдГЦЭМаЮЃЌЕЋВЛЪЧжааФЖдГЦЭМаЮЃЛ
ЃЈ2ЃЉбЁШЁ1ИіЭПЩЯвѕгАЃЌЪЙ4ИівѕгАаЁе§ЗНаЮзщГЩвЛИіжааФЖдГЦЭМаЮЃЌЕЋВЛЪЧжсЖдГЦЭМаЮЃЛ
ЃЈ3ЃЉбЁШЁ2ИіЭПЩЯвѕгАЃЌЪЙ5ИівѕгАаЁе§ЗНаЮзщГЩвЛИіжсЖдГЦЭМаЮЁЃ
ЃЈЧыНЋШ§ИіаЁЬтвРДЮзїД№дкЭМ1ЁЂЭМ2ЁЂЭМ3жаЃЌОљжЛашЛГіЗћКЯЬѕМўЕФвЛжжЧщаЮЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаХаЖЯЃК
ЂйвЛзщЖдБпЦНааЃЌСэвЛзщЖдБпЯрЕШЕФЫФБпаЮЪЧЦНааЫФБпаЮЃЎ
ЂкЖдНЧЯпЯрЕШЕФЫФБпаЮЪЧОиаЮЃЎ
ЂлЖдНЧаЮЛЅЯрДЙжБЧвЯрЕШЕФЫФБпаЮЪЧе§ЗНаЮЃЎ
ЂмгавЛЬѕЖдНЧЯпЦНЗжвЛИіФкНЧЕФЦНааЫФБпаЮЮЊСтаЮЃЎ
ЦфжаЃЌВЛе§ШЗЕФгаЃЈ ЃЉ
A.1Иі
B.2Иі
C.3Иі
D.4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
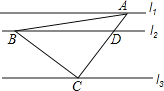
ЁОЬтФПЁПШчЭМЃЌжБЯпl1ЁЮl2ЁЮl3ЃЌвЛЕШбќжБНЧШ§НЧаЮABCЕФШ§ИіЖЅЕуAЃЌBЃЌCЗжБ№дкl1ЃЌl2ЃЌl3ЩЯЃЌЁЯACB=90ЁуЃЌACНЛl2гкЕуDЃЌвбжЊl1гыl2ЕФОрРыЮЊ1ЃЌl2гыl3ЕФОрРыЮЊ3ЃЌдђ![]() ЕФжЕЮЊЃЈ ЃЉ
ЕФжЕЮЊЃЈ ЃЉ
AЃЎ![]() BЃЎ
BЃЎ![]() CЃЎ
CЃЎ![]() DЃЎ
DЃЎ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧ(ЁЁ ЁЁ)
A. жБЯпABКЭжБЯпaВЛФмЪЧЭЌвЛЬѕжБЯп B. ЩфЯпABКЭЩфЯпBAЪЧСНЬѕЩфЯп
C. ЯпЖЮABКЭЯпЖЮBAЪЧСНЬѕЯпЖЮ D. жБЯпABКЭжБЯпBAЪЧСНЬѕжБЯп
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com