
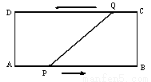
如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从A,C,同时出发,点P以2cm/s的速度向点B移动,到达B点后停止,点Q以1cm/s的速度向点D移动,到达D点后停止,P,Q两点出发后,经过_____________秒时,线段PQ的长是10cm.
 或8.
或8.
【解析】
试题分析:连接PQ,过Q作QM⊥AB,设经过x秒,线段PQ的长是10cm,根据题意可得PM=(16-3x)cm,QM=6cm,利用勾股定理可得 ,解方程得
,解方程得 .
.
故答案为: 或8.
或8.

考点:矩形的性质;勾股定理.
考点分析: 考点1:四边形 四边形:四边形的初中数学中考中的重点内容之一,分值一般为10-14分,题型以选择,填空,解答证明或融合在综合题目中为主,难易度为中。主要考察内容:①多边形的内角和,外角和等问题②图形的镶嵌问题③平行四边形,矩形,菱形,正方形,等腰梯形的性质和判定。突破方法:①掌握多边形,四边形的性质和判定方法。熟记各项公式。②注意利用四边形的性质进行有关四边形的证明。③注意开放性题目的解答,多种情况分析。 试题属性

科目:初中数学 来源:2014-2015学年福建省洛江区八年级上学期期末质量检测数学试卷(解析版) 题型:选择题
如图一,在边长为 的正方形中,挖掉一个边长为
的正方形中,挖掉一个边长为 的小正方形(
的小正方形( ),把余下的部分剪成一个矩形(如图二),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )
),把余下的部分剪成一个矩形(如图二),通过计算两个图形(阴影部分)的面积,验证了一个等式,则这个等式是( )


A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省巴中市平昌县九年级下学期第一次综合性阶段考试数学试卷(解析版) 题型:填空题
在平面直角坐标系中,如图,二次函数y=ax2+bx+c(a≠0)的图像与x轴交点的横坐标为x1、x2,其中–2< x1<-1,0< x2<1,则下列结论:①abc>0 ,②4a–2b+c<0,③当x>0时,函数值随x的增长而减少,④当x1<x<x2时,则y > 0.其中正确的是 (写出你认为正确的所有结论序号).

查看答案和解析>>
科目:初中数学 来源:2014-2015学年四川省巴中市平昌县九年级下学期第一次综合性阶段考试数学试卷(解析版) 题型:选择题
2013年,我国上海和安徽首先发现“H7N9”禽流感,H7N9是一种新型禽流感,其病毒颗粒呈多形性,其中球形病毒的最大直径为0.00000012米,这一直径用科学记数法表示为( ).
A.1.2×10﹣9米 B.1.2×10﹣8米
C.12×10﹣8米 D.1.2×10﹣7米
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省枣庄市九年级3月测试数学试卷(解析版) 题型:解答题
(本题7分)今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的两种统计图表.

对雾霾了解程度的统计表:
对雾霾的了解程度 | 百分比 |
A.非常了解 | 5% |
B.比较了解 | m |
C.基本了解 | 45% |
D.不了解 | n |
请结合统计图表,回答下列问题.
(1)本次参与调查的学生共有 人,m= ,n= ;
(2)请补全图中所示数的条形统计图;
(3)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”等级中的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,记下数字后放回袋中,另一人再从袋中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省枣庄市九年级3月测试数学试卷(解析版) 题型:选择题
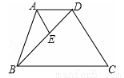
如图,梯形ABCD中,AD∥BC,AB=3,BC=4,连结BD,∠BAD的平分线交BD于 点E,且AE∥CD,则AD的长为( ).
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省枣庄市九年级3月测试数学试卷(解析版) 题型:选择题
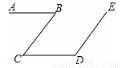
如图,AB∥CD,BC∥DE,若∠B=40°,则∠D的度数是( ).
A.40° B.140° C.160° D.60°
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省滨州市九年级下学期4月模拟数学试卷(解析版) 题型:解答题
(12分)如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0),B(4,0),C(0,2)三点
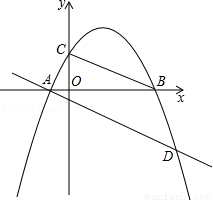
(1)求这条抛物线的解析式;
(2)E为抛物线上一动点,是否存在点E使以A、B、E为顶点的三角形与△COB相似?若存在,试求出点E的坐标;若不存在,请说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com