
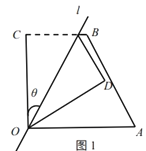
【题目】(阅读)如图1,四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,经过点
,经过点![]() 的直线
的直线![]() 将四边形分成两部分,直线
将四边形分成两部分,直线![]() 与
与![]() 所成的角设为
所成的角设为![]() ,将四边形
,将四边形![]() 的直角
的直角![]() 沿直线
沿直线![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,我们把这个操作过程记为
处,我们把这个操作过程记为![]() .
.
(理解)若点![]() 与点
与点![]() 重合,则这个操作过程为
重合,则这个操作过程为![]() [__________,__________];
[__________,__________];
(尝试)
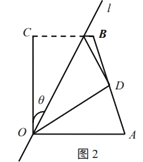
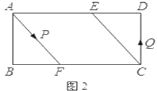
(1)若点![]() 恰为
恰为![]() 的中点(如图2),求
的中点(如图2),求![]() ;
;
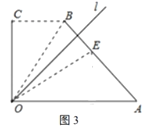
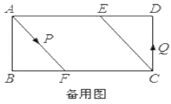
(2)经过![]() 操作,点
操作,点![]() 落在
落在![]() 处,若点
处,若点![]() 在四边形
在四边形![]() 的边
的边![]() 上(如图3),求出
上(如图3),求出![]() 的值.
的值.
【答案】![]() ;(1)30°;(2)5
;(1)30°;(2)5
【解析】
由题目条件可知,当点![]() 与点
与点![]() 重合时,
重合时,![]() =45°,
=45°,![]() ,即可得到结论;
,即可得到结论;
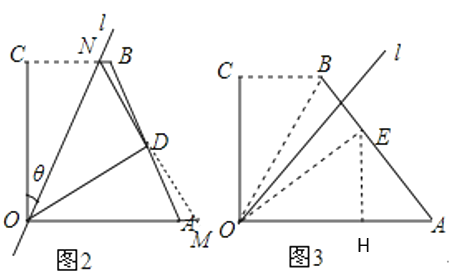
(1)见详解中图2,延长ND交OA的延长线于M ,根据折叠性质得![]() ,
,![]() ,由点D为AB的中点得到D点为MN的中点,所以OD垂直平分MN,则
,由点D为AB的中点得到D点为MN的中点,所以OD垂直平分MN,则![]() ,根据等腰三角形的性质得
,根据等腰三角形的性质得![]() ,则
,则![]() ,计算得到
,计算得到![]() ;
;
(2)见详解中图3,作EH⊥OA于H,根据折叠性质得AB⊥直线l,![]() ,由于
,由于![]() ,AB⊥直线l,即直线l平分∠AOC,则∠A=45°,所以△AHE为等腰直角三角形,则
,AB⊥直线l,即直线l平分∠AOC,则∠A=45°,所以△AHE为等腰直角三角形,则![]() ,所以
,所以![]() ,即
,即![]() .
.
理解:由题目条件可知,当点![]() 与点
与点![]() 重合时,
重合时,![]() =45°,
=45°,![]() ,所以
,所以![]() ;
;
(1)如图2,延长ND交OA的延长线于M,
∵四边形OABC的直角∠OCB沿直线l折叠,点C落在点D处,
∴![]() ,
,![]() ,
,
∵点D为AB的中点,
∴D点为MN的中点,
∴OD垂直平分MN,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
(2)如图3,作ED⊥OA于D,
∵四边形OABC的直角∠OCB沿直线l折叠后,点B落在点四边形OABC的边AB上的E处,
∴AB⊥直线l,![]() ,
,
∵![]() ,AB⊥直线l,
,AB⊥直线l,
即直线l平分∠AOC,
∴∠A=45°,
∴△ADE为等腰直角三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为: ![]() ;(1)30°;(2)5
;(1)30°;(2)5


科目:初中数学 来源: 题型:
【题目】某校组织一项公益知识竞赛,比赛规定:每个班级由2名男生、2名女生及1名班主任老师组成代表队.但参赛时,每班只能有3名队员上场参赛,班主任老师必须参加,另外2名队员分别在2名男生和2名女生中各随机抽出1名.初三(1)班由甲、乙2名男生和丙、丁2名女生及1名班主任组成了代表队,求恰好抽到由男生甲、女生丙和这位班主任一起上场参赛的概率.(请用“画树状图”或“列表”或“列举”等方法给出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店只销售某种进价为40元/kg的产品,已知该店按60元kg出售时,每天可售出100kg,后来经过市场调查发现,单价每降低1元,则每天的销售量可增加10kg.
(1)若单价降低2元,则每天的销售量是_____千克,每天的利润为_____元;若单价降低x元,则每天的销售量是_____千克,每天的利润为______元;(用含x的代数式表示)
(2)若该店销售这种产品计划每天获利2240元,单价应降价多少元?
(3)当单价降低多少元时,该店每天的利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
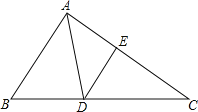
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠CAB=70°,在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得C′C∥AB,则∠CAB'等于( )
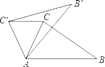
A. 30°B. 25°C. 15°D. 10°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司欲招聘一名部门经理,对甲、乙、丙三名候选人进行了三项素质测试.各项测试成绩如表格所示:
测试项目 | 测试成绩 | ||
甲 | 乙 | 丙 | |
专业知识 | 74 | 87 | 90 |
语言能力 | 58 | 74 | 70 |
综合素质 | 87 | 43 | 50 |
(1)如果根据三次测试的平均成绩确定人选,那么谁将被录用?
(2)根据实际需要,公司将专业知识、语言能力和综合素质三项测试得分按4:3:1的比例确定每个人的测试总成绩,此时谁将被录用?
(3)请重新设计专业知识、语言能力和综合素质三项测试得分的比例来确定每个人的测试总成绩,使得乙被录用,若重新设计的比例为x:y:1,且x+y+1=10,则x= ,y= .(写出x与y的一组整数值即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 、
、![]() 边上的点,
边上的点,![]() 与
与![]() 交于点
交于点![]() .
.
(1)如图1,若四边形![]() 是正方形,且
是正方形,且![]() ,求证:
,求证:![]() ;
;
(2)如图2,若四边形![]() 是菱形,试探究当
是菱形,试探究当![]() 与
与![]() 满足什么关系,使得
满足什么关系,使得![]() ;
;
(3)如图3,![]() ,
,![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的数量关系,请说明理由.
的数量关系,请说明理由.

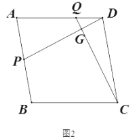

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,矩形![]() 中,
中,![]() ,
,![]() 的垂直平分
的垂直平分![]() 线分别交
线分别交![]() 于点
于点![]() ,垂足为
,垂足为![]() .
.
(1)如图1,连接![]() ,求证:四边形
,求证:四边形![]() 为菱形;
为菱形;
(2)如图2,动点![]() 分别从
分别从![]() 两点同时出发,沿
两点同时出发,沿![]() 和
和![]() 各边匀速运动一周,即点
各边匀速运动一周,即点![]() 自
自![]() 停止,点
停止,点![]() 自
自![]() 停止.在运动过程中,
停止.在运动过程中,
①已知点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,运动时间为
,运动时间为![]() 秒,当
秒,当![]() 四点为顶点的四边形是平行四边形时,则
四点为顶点的四边形是平行四边形时,则![]() ____________.
____________.
②若点![]() 的运动路程分别为
的运动路程分别为![]() (单位:
(单位:![]() ),已知
),已知![]() 四点为顶点的四边形是平行四边形,则
四点为顶点的四边形是平行四边形,则![]() 与
与![]() 满足的数量关系式为____________.
满足的数量关系式为____________.
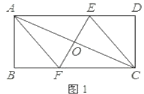
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com