

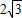 cm
cm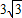 cm
cm cm
cm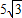 cm
cm科目:初中数学 来源: 题型:
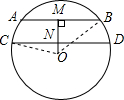 在直径为50cm的圆中,弦AB为40cm,弦CD为48cm,且AB∥CD,求AB与CD之间距离.
在直径为50cm的圆中,弦AB为40cm,弦CD为48cm,且AB∥CD,求AB与CD之间距离.| 1 |
| 2 |
| 1 |
| 2 |
| OB2-BM2 |
| 252-202 |
| OC2-CN2 |
| 252-242 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
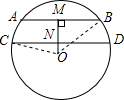 在直径为50cm的圆中,弦AB为40cm,弦CD为48cm,且AB∥CD,求AB与CD之间距离.
在直径为50cm的圆中,弦AB为40cm,弦CD为48cm,且AB∥CD,求AB与CD之间距离. AB=
AB= ×40=20cm,
×40=20cm,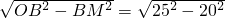 =15cm.
=15cm.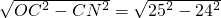 =7cm,
=7cm,查看答案和解析>>
科目:初中数学 来源:《24.1.1 圆及垂径定理》2009年同步练习(解析版) 题型:解答题
 AB=
AB= ×40=20cm,
×40=20cm,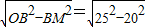 =15cm.
=15cm.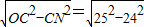 =7cm,
=7cm,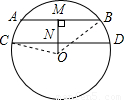
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com