
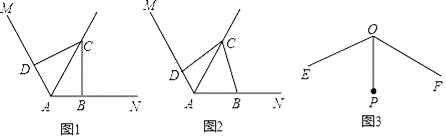
【题目】已知∠MAN=120°,点C是∠MAN的平分线AQ上的一个定点,点B,D分别在AN,AM上,连接BD.
【发现】
(1)如图1,若∠ABC=∠ADC=90°,则∠BCD= °,△CBD是 三角形;
【探索】
(2)如图2,若∠ABC+∠ADC=180°,请判断△CBD的形状,并证明你的结论;
【应用】
(3)如图3,已知∠EOF=120°,OP平分∠EOF,且OP=1,若点G,H分别在射线OE,OF上,且△PGH为等边三角形,则满足上述条件的△PGH的个数一共有 .(只填序号)
①2个②3个③4个④4个以上
【答案】(1)60,等边;(2)等边三角形,证明见解析(3)④.
【解析】试题分析:(1)利用四边形的内角和即可得出∠BCD的度数,再利用角平分线的性质定理即可得出CB,即可得出结论;
(2)先判断出∠CDE=∠ABC,进而得出△CDE≌△CFB(AAS),得出CD=CB,再利用四边形的内角和即可得出∠BCD=60°即可得出结论;
(3)先判断出∠POE=∠POF=60°,先构造出等边三角形,找出特点,即可得出结论.
试题解析:(1)如图1,连接BD,
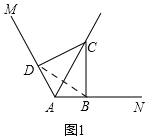
∵∠ABC=∠ADC=90°,∠MAN=120°,
根据四边形的内角和得,∠BCD=360°-(∠ABC+∠ADC+∠MAN)=60°,
∵AC是∠MAN的平分线,CD⊥AM.CB⊥AN,
∴CD=CB,(角平分线的性质定理),
∴△BCD是等边三角形;
故答案为:60,等边;
(2)如图2,同(1)得出,∠BCD=60°(根据三角形的内角和定理),
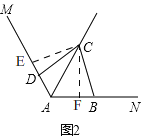
过点C作CE⊥AM于E,CF⊥AN于F,
∵AC是∠MAN的平分线,
∴CE=CF,
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°,
∴∠CDE=∠ABC,
在△CDE和△CFB中,
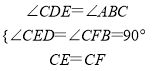 ,
,
∴△CDE≌△CFB(AAS),
∴CD=CB,
∵∠BCD=60°,
∴△CBD是等边三角形;
(3)如图3,
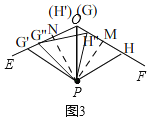
∵OP平分∠EOF,∠EOF=120°,
∴∠POE=∠POF=60°,在OE上截取OG'=OP=1,连接PG',
∴△G'OP是等边三角形,此时点H'和点O重合,
同理:△OPH是等边三角形,此时点G和点O重合,
将等边△PHG绕点P逆时针旋转到等边△PG'H',在旋转的过程中,
边PG,PH分别和OE,OF相交(如图中G',H')和点P围成的三角形全部是等边三角形,(旋转角的范围为(0°到60°包括0°和60°),
所以有无数个;
理由:同(2)的方法.
故答案为④.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别相交于点
轴分别相交于点![]() 、点
、点![]() ,
,![]() ,若将
,若将![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合,折痕
重合,折痕![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 交于点
交于点![]() .
.
(1)求![]() 的值;
的值;
(2)求点![]() 的坐标;
的坐标;
(3)求直线![]() 的表达式.
的表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市对城区部分路段的人行道地砖、绿化带、排水管等公用设施进行全面更新改造,根据市政建设的需要,需在35天内完成工程.现有甲、乙两个工程队有意承包这项工程,经调查知道,乙工程队单独完成此项工程的时间是甲工程队单独完成此项工程时间的2倍,若甲、乙两工程队合作,只需10天完成.
(1)甲、乙两个工程队单独完成此项工程各需多少天?
(2)若甲工程队每天的工程费用是4万元,乙工程队每天的工程费用是2.5万元,请你设计一种方案,既能按时完工,又能使工程费用最少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】温度与我们的生活息息相关,如图是一个温度计实物示意图,左边的刻度是摄氏温度(℃),右边的刻度是华氏温度(℉).设摄氏温度为x(℃)华氏温度为y(℉),则y是x的一次函数,通过观察我们发现,温度计上的摄氏温度为0℃时,华氏温度为32℉;摄氏温度为﹣20℃时,华氏温度为﹣4℉

请根据以上信息,解答下列问题
(1)仔细观察图中数据,试求出y与x的函数关系式;
(2)当摄氏温度为﹣5℃时,华氏温度为多少?
(3)当华氏温度为59℉时,摄氏温度为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,在AC边上取两点M、N,使∠MBN=30°.若AM=m,MN=x,CN=n,则以x,m,n为边长的三角形的形状为( )
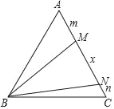
A. 锐角三角形 B. 直角三角形
C. 钝角三角形 D. 随x,m,n的值而定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】精准扶贫,助力苹果产业大发展.甲、乙两超市为响应党中央将消除贫困和实现共同富裕作为重要的奋斗目标,到种植苹果的贫困山区分别用![]() 元以相同的进价购进质量相同的苹果.甲超市的销售方案:将苹果按大小分类包装销售,其中大苹果
元以相同的进价购进质量相同的苹果.甲超市的销售方案:将苹果按大小分类包装销售,其中大苹果![]() 千克,以进价的
千克,以进价的![]() 倍价格销售,剩下的小苹果以高于进价的
倍价格销售,剩下的小苹果以高于进价的![]() 销售.乙超市的销售方案:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利
销售.乙超市的销售方案:不将苹果按大小分类,直接包装销售,价格按甲超市大、小两种苹果售价的平均数定价.若两超市将苹果全部售完,其中甲超市获利![]() 元(包含人工工资和运费).
元(包含人工工资和运费).
(1)苹果进价为每千克多少元?
(2)乙超市获利多少元?并比较哪种销售方式更合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
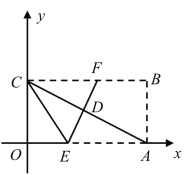
【题目】如图,把长方形纸片![]() 放入平面直角坐标系中,使
放入平面直角坐标系中,使![]() 分别落在
分别落在![]() 轴的的正半轴上,连接
轴的的正半轴上,连接![]() ,且
,且![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)将纸片![]() 折叠,使点
折叠,使点![]() 与点
与点![]() 重合(折痕为
重合(折痕为![]() ),求折叠后纸片重叠部分
),求折叠后纸片重叠部分![]() 的面积;
的面积;
(3)求![]() 所在直线的函数表达式,并求出对角线
所在直线的函数表达式,并求出对角线![]() 与折痕
与折痕![]() 交点
交点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com