
分析 (1)分x≥1和x<1两种情形,把绝对值方程转化为一元二次方程解决.
(2)①当m=n时,$\frac{n}{m}$+$\frac{m}{n}$=2;
②当m≠n时,m、n是方程x2-7x+2=0的两根,根据根与系数关系即可解决问题.
解答 解:(1)当x≥1时,原方程化为x2-x-2=0,解得:x1=2,x2=-1(不合题意,舍去);
当x<1时,原方程化为x2+x-4=0,解得:x1=$\frac{-1-\sqrt{17}}{2}$,x2=$\frac{-1+\sqrt{17}}{2}$(不合题意,舍去),;
∴原方程的根是x1=2,x2=$\frac{-1-\sqrt{17}}{2}$.
(2)∵m2-7m+2=0,n2-7n+2=0,
①当m=n时,$\frac{n}{m}$+$\frac{m}{n}$=2,
②当m≠n时,m、n是方程x2-7x+2=0的两根,
∴m+n=7,mn=2,
∴原式=$\frac{(m+n)^{2}-2mn}{mn}$=$\frac{49-4}{2}$=$\frac{45}{2}$.
∴$\frac{n}{m}$+$\frac{m}{n}$的值为2或$\frac{45}{2}$.
点评 本题考查根与系数关系、整体代入的思想,解题的关键是学会转化的思想,把问题转化为一元二次方程解决,学会分类讨论的思想,学会利用公式恒等变形,属于中考常考题型.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:选择题
| A. | (4,-3) | B. | (-4,3) | C. | (0,-3) | D. | (0,3) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
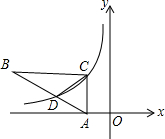 如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )
如图Rt△ABC在平面坐标系中,顶点A在x轴上,∠ACB=90°,CB∥x轴,双曲线y=$\frac{k}{x}$经过C点及AB的三等点D(BD=2AD),S△BCD=6,则k的值为( )| A. | 3 | B. | 6 | C. | -3 | D. | -6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 了解某校九(1)班学生视力情况 | B. | 调查2016年央视春晚的收视率 | ||
| C. | 检测一批电灯泡的使用寿命 | D. | 了解我市中学生课余上网时间 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )
如图,在4×4正方形网格中,任选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形的概率是( )| A. | $\frac{6}{13}$ | B. | $\frac{5}{13}$ | C. | $\frac{4}{13}$ | D. | $\frac{3}{13}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com