
【题目】如图,正方形![]() 中,点
中,点![]() 、
、![]() 分别在边
分别在边![]() 、
、![]() 上,且
上,且![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中正确的是________(只填写序号).
;其中正确的是________(只填写序号).

【答案】①②③
【解析】
由已知得AB=AD,AE=AF,利用“HL”可证ΔABE![]() ΔADF,利用全等的性质判断①②③正确,在AD上取一点G,连接FG,使AG=GF,由正方形,等边三角形的性质可知∠DAF=15°,从而得∠DGF=30°,设DF=1,则AG=GF=2,DG=
ΔADF,利用全等的性质判断①②③正确,在AD上取一点G,连接FG,使AG=GF,由正方形,等边三角形的性质可知∠DAF=15°,从而得∠DGF=30°,设DF=1,则AG=GF=2,DG=![]() ,分别表示AD,CF, EF的长即可判断④是否正确.
,分别表示AD,CF, EF的长即可判断④是否正确.
解:∵AB=AD,AE=AF=EF,
∴ΔABEΔADF(HL),ΔAEF为等边三角形,
∴BE=DF,
又BC=CD,
∴CE=CF,
∴∠BAE=![]() (∠BAD∠EAF)=
(∠BAD∠EAF)= ![]() (90°60°)=15°
(90°60°)=15°
∴∠AEB=90°∠BAE=75°
∴∠AEB=90°∠BAE=75°,
∴①②③正确,
如图:在AD上取一点G,连接FG,使AG=GF,

则∠DAF=∠GFA=15°,
∴∠DGF=2∠DAF=30°,
设DF=1,则AG=GF=2,DG=![]() ,
,
∴AD=CD=2+![]() ,CF=CE=CDDF=1+
,CF=CE=CDDF=1+![]() ,
,
∴EF=![]() CF=
CF=![]() ,而BE+DF=2,
,而BE+DF=2,
∴BE+DF![]() EF
EF
即④错误,
故答案为:①②③


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=10,BC=4,Q为AB边的中点,P为CD边上的动点,且△AQP是腰长为5的等腰三角形,则CP的长为_______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边三角形![]() 的高为6,在这个三角形所在的平面内有一个点
的高为6,在这个三角形所在的平面内有一个点![]() ,若点
,若点![]() 到
到![]() 的距离是1,点
的距离是1,点![]() 到
到![]() 的距离是2,则点
的距离是2,则点![]() 到
到![]() 的最小距离与最大距离分别是_______.
的最小距离与最大距离分别是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() ,把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点
,把一条长为2019个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点![]() 处,并按
处,并按![]() 的规律紧绕在四边形
的规律紧绕在四边形![]() 的边上,则细线另一端所在位置的点的坐标是( )
的边上,则细线另一端所在位置的点的坐标是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图①,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(![]() ,0),B(3,0),与y轴交于点C,连接BC.
,0),B(3,0),与y轴交于点C,连接BC.
(1)求抛物线的表达式;
(2)抛物线上是否存在点M,使得△MBC的面积与△OBC的面积相等,若存在,请直接写出点M的坐标;若不存在,请说明理由;
(3)点D(2,m)在第一象限的抛物线上,连接BD.在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P的坐标;如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校提倡练字,小冬和小红一起去文具店买钢笔和字帖,小冬在文具店买1支钢笔和3本字帖共花了38元,小红买了2支钢笔和4本字帖共花了64元.
(1)每支钢笔与每本字帖分别多少元?
(2)帅帅在六一节当天去买,正巧碰到文具店搞促销,促销方案有两种形式:
①所购商品均打九折
②买一支钢笔赠送一本字帖
帅帅要买5支钢笔和15本字帖,他有三种选择方案:
(Ⅰ)一次买5支钢笔和15本字帖,然后按九折付费;
(Ⅱ)一次买5支钢笔和10本字帖,文具店再赠送5本字帖;
(Ⅲ)分两次购买,第一次买5支钢笔,文具店会赠送5本字帖,第二次再去买10本字帖,可以按九折付费;问帅帅最少要付多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(1,1),B(4,1),C(3,3).
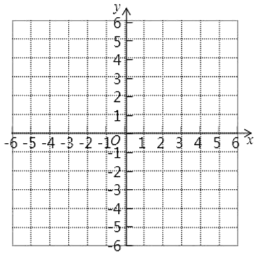
(1)先作出△ABC,再将△ABC向下平移5个单位长度后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O逆时针旋转90°后得得到△A2B2C2,请画出△A2B2C2;
(3)求出以O,A1,B为顶点的三角形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com